已知θ为第四象限角.且sinθ=$\frac{x+2}{2x+1}$.则实数x的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

12．已知θ为第四象限角，且sinθ=$\frac{x+2}{2x+1}$，则实数x的取值范围是（-2，-1）．

分析由正弦函数在第四限的取值范围是[-1，0），能求出实数x的取值范围．

解答解：∵θ为第四象限角，且sinθ=$\frac{x+2}{2x+1}$，
∴-1＜$\frac{x+2}{2x+1}$＜0，
解得-2＜x＜-1．
∴实数x的取值范围是（-2，-1）．
故答案为：（-2，-1）．

点评本题考查实数的取值范围的求法，是基础题，解题时要认真审题，注意正弦函数的性质的合理运用．

练习册系列答案

单元测评卷精彩考评七年级下数学延边教育出版社系列答案

$-\frac{{\sqrt{6}}}{4}$

B．

$-\frac{{\sqrt{2}}}{4}$

C．

$\frac{{\sqrt{6}}}{4}$

D．

$\frac{{\sqrt{2}}}{4}$

3．若（1-2015x）²⁰¹⁵=a₀+a₁x+…+a₂₀₁₅x²⁰¹⁵（x∈R），则$\frac{a_1}{2015}$+$\frac{a_2}{2015^2}$+…+$\frac{a_{2015}}{2015^{2015}}$的值为-1．

20．数列{2n-11}的前n项和S_n中最小的是（　　）

S₄

S₅

S₆

S₇

7．若执行如图所示的程序，输出的结果为48，则判断框中应填入的条件为（　　）

17．（1）己知cosθ=$\frac{12}{13}$，且θ为第四象限角，求sinθ和tanθ；
（2）已知sinx=-$\frac{1}{3}$，求cosx和tanx．
（3）已知tanα=3，π＜α＜$\frac{3}{2}$π，求cosα-sinα的值．

4．

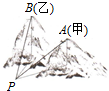如图，某人在山脚P处测得甲山山顶A的仰角为30°，乙山山顶B的仰角为45°，∠APB的大小为45°，山脚P到山顶A的直线距离为2km，在A处测得山顶B的仰角为30°，则乙山的高度为2km．

1．执行如图所示的程序框图．若输出的结果为-1，则可以输入的x的个数为（　　）

2．在抛物线y²=2px（p＞0）中有如下结论：过焦点F的动直线l交抛物线y²=2px（p＞0）于A、B两点，则$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{2}{p}$为定值，请把此结论类比到椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）中有：过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点F的直线交椭圆于A，B则$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{2a}{b^2}$为定值；当椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1时，$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{4}{3}$．

试题分类