题目内容
15.已知幂函数的图象过点(2,16)和($\frac{1}{2}$,m),则m=$\frac{1}{16}$.分析 设出幂函数的解析式,用待定系数法求出解析式,再计算m的值.
解答 解:设幂函数的解析式为y=xa,其图象过点(2,16),
则2a=16,
解得a=4,即y=x4;
又图象过点($\frac{1}{2}$,m),
则m=${(\frac{1}{4})}^{4}$=$\frac{1}{16}$.
故答案为:$\frac{1}{16}$.
点评 本题考查了用待定系数法求幂函数解析式的应用问题,是基础题目.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.下列两个函数相同的是( )
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
10.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤2}\\{x-y≤2}\end{array}\right.$,若不等式y≥ax-3恒成立,则实数a的取值范围为( )
| A. | (-∞,$\frac{3}{2}$] | B. | (-∞,4] | C. | [$\frac{3}{2}$,2] | D. | [2,4] |
20.数列{2n-11}的前n项和Sn中最小的是( )
| A. | S4 | B. | S5 | C. | S6 | D. | S7 |
7.若执行如图所示的程序,输出的结果为48,则判断框中应填入的条件为( )


| A. | i≥6? | B. | i>6? | C. | i≥4? | D. | i>4? |
5.函数y=lnx-6+2x的零点为x0,x0∈( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (5,6) |
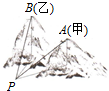 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.