题目内容
16.已知经过点M(-5,0)的直线l与圆x2+(y+1)2=25相切,那么直线l的方程为x=-5或12x-5y+60=0.分析 把圆的方程化为标准方程,找出圆心坐标和半径r,直线与圆相切,所以圆心到直线的距离d等于半径r,分类讨论,利用点到直线的距离公式表示出d,让d等于r列出关于k的方程,求出方程的解即可确定出切线方程,综上得到两条满足题意的切线方程.
解答 解:圆x2+(y+1)2=25的圆心坐标为(0,-1),半径r=5,
斜率不存在时,此时过点M(-5,0)的切线方程为x=-5;
设切线的斜率为k,由切线过(-5,0),得到切线方程为:y=k(x+5),即kx-y+5k=0,
则有圆心到切线的距离d=$\frac{|1+5k|}{\sqrt{{k}^{2}+1}}$=r=5,解得k=$\frac{12}{5}$,
所以切线方程为:12x-5y+60=0,
综上,所求切线的方程为x=-5或12x-5y+60=0.
故答案为:x=-5或12x-5y+60=0.
点评 此题考查了直线与圆相切满足的关系,同时要求学生灵活运用点到直线的距离公式,会把圆的方程化为标准方程,会从圆的标准方程找出圆心坐标和圆的半径,掌握当直线与圆相切时,圆心到直线的距离等于圆的半径是解本题的关键.

练习册系列答案
相关题目
6.下列两个函数相同的是( )
| A. | f(x)=lnx2,g(x)=2lnx | B. | f(x)=x,g(x)=($\sqrt{x}$)2 | ||
| C. | f(x)=cosx•tanx,g(x)=sinx | D. | f(x)=x2,g(x)=$\sqrt{{x}^{4}}$ |
7.若执行如图所示的程序,输出的结果为48,则判断框中应填入的条件为( )


| A. | i≥6? | B. | i>6? | C. | i≥4? | D. | i>4? |
1.执行如图所示的程序框图.若输出的结果为-1,则可以输入的x的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
8.与向量$\overrightarrow{a}$=(1,3,-2)平行的一个向量的坐标是( )
| A. | ($\frac{1}{3}$,1,1) | B. | (-$\frac{1}{2}$,-$\frac{3}{2}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$,-1) | D. | ($\sqrt{2}$,-3,-2$\sqrt{2}$) |
5.函数y=lnx-6+2x的零点为x0,x0∈( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (5,6) |
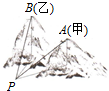 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.