题目内容
13.已知点A(0,2),抛物线y2=2px(p>0)的焦点为F,准线为l,线段FA交抛物线于点B,过B作准线l的垂线,垂足为M,若AM⊥MF,求p的值.分析 由抛物线的定义可得BM=BF,又 AM⊥MF,根据直角三角形斜边的中点是外心可得故B 为线段AF的中点,求出B的坐标代入抛物线方程求得 p值.
解答 解:由抛物线的定义可得BM=BF,F($\frac{1}{2}$p,0),又 AM⊥MF,故B为线段AF的中点,
∴B($\frac{1}{4}$p,1),
把B($\frac{1}{4}$p,1)代入抛物线y2=2px(p>0)得,
1=2p×$\frac{1}{4}$p,
∴p=$\sqrt{2}$
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,判断B为线段AF的中点,是解题的关键,属于中档题.

练习册系列答案
相关题目
1.执行如图所示的程序框图.若输出的结果为-1,则可以输入的x的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
8.与向量$\overrightarrow{a}$=(1,3,-2)平行的一个向量的坐标是( )
| A. | ($\frac{1}{3}$,1,1) | B. | (-$\frac{1}{2}$,-$\frac{3}{2}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$,-1) | D. | ($\sqrt{2}$,-3,-2$\sqrt{2}$) |
5.函数y=lnx-6+2x的零点为x0,x0∈( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (5,6) |
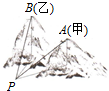 如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.
如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为2km,在A处测得山顶B的仰角为30°,则乙山的高度为2km.