题目内容
甲、乙两个进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止,设甲在每局中获胜的概率为
,乙在每局中获胜的概率为
,且各局胜负相互独立.
(1)求甲在打的局数最少的情况下获胜的概率;
(2)求比赛停止时已打局数ξ的期望.
| 2 |
| 3 |
| 1 |
| 3 |
(1)求甲在打的局数最少的情况下获胜的概率;
(2)求比赛停止时已打局数ξ的期望.
考点:离散型随机变量的期望与方差
专题:应用题,概率与统计
分析:(1)由甲在每局中获胜的概率为
,可得甲在打的局数最少的情况下获胜的概率;
(2)ξ的所有可能值为2,4,6.设每两局比赛为一轮,求出该轮结束时比赛停止的概率,由此能求出ξ的分布列,由ξ的分布列能求出Eξ.
| 2 |
| 3 |
(2)ξ的所有可能值为2,4,6.设每两局比赛为一轮,求出该轮结束时比赛停止的概率,由此能求出ξ的分布列,由ξ的分布列能求出Eξ.
解答:
解:(1)甲在打两局的情况下获胜的概率为P=
×
=
;
(2)ξ的可能取值为2、4、6,则PP(ξ=2)=(
)2+(
)2=
,
P(ξ=4)=
•
•
•[(
)2+(
)2]=
,P(ξ=6)=
(
)2(
)2=
,
故ξ的分布列为
ξ的期望Eξ=2×
+4×
+6×
=
.
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
(2)ξ的可能取值为2、4、6,则PP(ξ=2)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 5 |
| 9 |
P(ξ=4)=
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 20 |
| 81 |
| C | 1 2 |
| C | 1 2 |
| 2 |
| 3 |
| 1 |
| 3 |
| 16 |
| 81 |
故ξ的分布列为
| ξ | 2 | 4 | 6 | ||||||
| P |
|
|
|
| 5 |
| 9 |
| 20 |
| 81 |
| 16 |
| 81 |
| 266 |
| 81 |
点评:本题考查互斥事件的概率和公式、考查相互独立事件同时发生的概率乘法公式、考查事随机变量的分布列的求法、考查随机变量的期望公式.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
若集合A={x|-1≤2x+1≤3},B={x|
≤2},则A∩B=( )
| x-2 |
| x |
| A、{x|-1≤x<0} |
| B、{x|0<x≤1} |
| C、{x|0≤x≤2} |
| D、{x|0≤x≤1} |
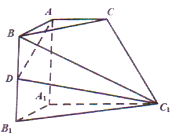 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.