题目内容
曲线y=3lnx+x在点（1，1）处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：根据函数的导数的几何意义，求出导数后代入该点横坐标，即可求出切线斜率．然后求出切线方程．
解答：
解：曲线y=3lnx+x，
∴y′=
+1，
∴曲线y=3lnx+x在点（1，1）处的切线的斜率是：4．
曲线y=3lnx+x在点（1，1）处的切线方程为：y-1=4（x-1），即4x-y-3=0．
故答案为：4x-y-3=0．
∴y′=
| 3 |
| x |
∴曲线y=3lnx+x在点（1，1）处的切线的斜率是：4．
曲线y=3lnx+x在点（1，1）处的切线方程为：y-1=4（x-1），即4x-y-3=0．
故答案为：4x-y-3=0．
点评：本题考查函数导数的基本运算，导数的几何意义，切线方程的求法，考查计算能力．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
等差数列{an}中，已知a1=
，a3+a6=3，an=7，则n为（ ）
| 1 |
| 3 |
| A、19 | B、20 | C、21 | D、22 |
设函数f（x）=（1+x）α的定义域是[-1，+∞），其中常数α＞0．
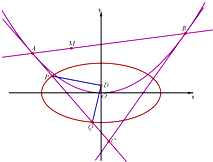已知抛物线C2：x2=2py（p＞0）的通径长为4，椭圆C1：