题目内容

已知两直线l1：2x-y+4=0，l2：3x+5y-2=0的交点为P，求过点P且过点（0，-1）的直线方程．
考点：两条直线的交点坐标,直线的两点式方程
专题：直线与圆
分析：联立直线方程求出交点坐标，利用两点式求出直线方程即可．
解答： 解：两直线l1：2x-y+4=0，l2：3x+5y-2=0的交点为P，
∴
2x-y+4=0
3x+5y-2=0
，解得
x=-
18
13
y=
16
13
，P（-
18
13
，
16
13
）．
∴过点P且过点（0，-1）的直线方程为：
y+1
-1-
16
13
=
x
18
13
，
即：29x+18y+18=0．
点评：本题考查直线的交点坐标的求法，两点式方程的求法，解决此类问题的方法是联立两条直线的方程进行计算，要细心仔细．
练习册系列答案
相关题目
甲、乙两个进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止，设甲在每局中获胜的概率为
2
3
，乙在每局中获胜的概率为
1
3
，且各局胜负相互独立．
（1）求甲在打的局数最少的情况下获胜的概率；
（2）求比赛停止时已打局数ξ的期望．
若函数f（x）=ax3+3x2-x恰好有三个单调区间，那么a的取值范围是
 
．
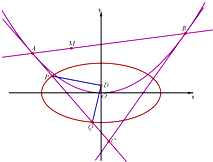已知抛物线C2：x2=2py（p＞0）的通径长为4，椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，且过抛物线C2的焦点．
（1）求抛物线C2和椭圆C1的方程；
（2）过定点M（-1，
3
2
）引直线l交抛物线C2于A，B两点（点A在点B的左侧），分别过A、B作抛物线C2的切线l1，l2，且l1与椭圆C1相交于P，Q两点．记此时两切线l1，l2的交点为点C．
①求点C的轨迹方程；
②设点D（0，
1
4
），求△DPQ的面积的最大值，并求出此时点C的坐标．
已知f（x）=x-e 
x
a
存在单调递减区间．
（Ⅰ）求实数a的取值范围；
（Ⅱ）判断曲线y=f（x）在x=0的切线能否与曲线y=ex相切？若存在，求出a，若不存在，说明理由；
（Ⅲ）若f（x1）=f（x2）=0（x1＜x2），求证：
x1
x2
＜
e
a
．
已知定义在R上的偶函数，并且满足f（x+2﹚=-
1
f(x)
．
（1）当2≤x≤3时，f（x）=x，试求f（105.5）的值；
（2）当x∈[0，2]时，f（x）=2x-1 试求当x∈﹙6，10﹚时，f（x）的解析式．
求函数f（x）=-
1
2
x2+x+3在区间[t，t+2]的最大值．
若函数f（x）=asinx+cosx的图象关于点（-
π
3
，0）成中心对称，则a=
 
．
在数列{an}中，an=-n2+λn，且{an}为递减数列，则λ的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网