题目内容
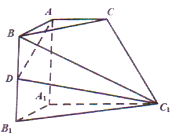 如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.
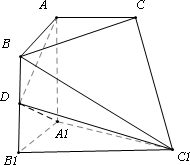
如图所示的六面体,面ABC∥面A1B1C1,AA1⊥面ABC,AA1=A1C1=2AB=2A1B1=2AC=2,AD⊥DC1,D为BB1的中点.(1)求证:AB⊥AC;
(2)求四面体C1-ADC的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:常规题型,空间位置关系与距离
分析:(1)要证AB⊥AC,由于A1C1∥AC,可以转化为证明A1C1⊥AB,通过证明A1C1⊥面ABB1 A1,可以证明A1C1⊥AB;
(2)要求四面体C1-ADC的体积,可以转化为求四面体D-ACC1 的体积.
(2)要求四面体C1-ADC的体积,可以转化为求四面体D-ACC1 的体积.
解答:
解:(1)证明:连结DA1,由题意得,面ABB1 A1 为矩形,
∵AA1=2AB=2A1B1
∴AD⊥DA1
因为AD⊥DC1,A1 D∩DC1=D,
所以AD⊥面DC1 A1,得AD⊥A1C1
所以A1C1⊥面ABB1 A1,
∵AB?面ABB1 A1,
∴A1C1⊥AB
又∵A1C1∥AC
∴AB⊥AC.
(2)V C1-ADC=VD-ACC1=
.
所以四面体C1-ADC的体积为
.
∵AA1=2AB=2A1B1
∴AD⊥DA1
因为AD⊥DC1,A1 D∩DC1=D,
所以AD⊥面DC1 A1,得AD⊥A1C1
所以A1C1⊥面ABB1 A1,
∵AB?面ABB1 A1,
∴A1C1⊥AB
又∵A1C1∥AC
∴AB⊥AC.
(2)V C1-ADC=VD-ACC1=
| 1 |
| 3 |
所以四面体C1-ADC的体积为
| 1 |
| 3 |

点评:本题考查了线面位置关系的证明及几何体的体积,证明线线垂直一般转化成证明线面垂直;求三棱锥的体积关键是通过转换顶点转化成易求底面积和高的三棱锥的体积问题.

练习册系列答案
相关题目
在△ABC中
=
,
=
,则
+
等于( )
| AB |
| a |
| BC |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,已知PA⊥面ABCD,PA=AB=AD=
如图,已知PA⊥面ABCD,PA=AB=AD= 设函数f(x)=(1+x)α的定义域是[-1,+∞),其中常数α>0.
设函数f(x)=(1+x)α的定义域是[-1,+∞),其中常数α>0.