题目内容

求证：
C
0
n
+
2C
1
n
+3
C
2
n
+…+(n+1
)C
n
n
=2n+n•2n-1．
考点：二项式系数的性质
专题：二项式定理
分析：直接采用倒序相加法再结合组合数的性质即可证明结论；
解答： 证明：记S=
C
0
n
+
2C
1
n
+3
C
2
n
+…+(n+1
)C
n
n
，
       倒序则S=（n+1）Cnn+nCnn-1+…+
C
0
n
，
∴2S=（n+2）cn0+（n+2）Cn1+…+（n+2）Cnn=（n+2）•2n
∴S=2n+n•2n-1．
点评：本题考查倒序相加求和及二项式系数的性质，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=aex，g（x）=lnx-lna，其中a为常数，且函数y=f（x）和y=g（x）的图象在它们与坐标轴交点处的切线互相平行．
（Ⅰ）求常数a的值；
（Ⅱ）若存在x∈[0，+∞），使不等式
x-m
f(x)
＞x成立，求实数m的取值范围；
（Ⅲ）令u（x）=|f（x）-g（x）|，求证：u（x）＞2．
甲、乙两个进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止，设甲在每局中获胜的概率为
2
3
，乙在每局中获胜的概率为
1
3
，且各局胜负相互独立．
（1）求甲在打的局数最少的情况下获胜的概率；
（2）求比赛停止时已打局数ξ的期望．
设函数f（x）=（1+x）α的定义域是[-1，+∞），其中常数α＞0．
（1）若α＞1，求y=f（x）的过原点的切线方程．
（2）当α＞2时，求最大实数A，使不等式f（x）＞1+αx+Ax2对x＞0恒成立．
（3）证明当α＞1时，对任何n∈N*，有1＜
1
n
n+1
k=2
（（
k-1
k
）α+
α
k
）＜α．
在等比数列{an}中，公比为q，前m项和为Sm（Sm≠0），证明：Sm，S2m-Sm，S3m-S2m，…，Skm-S（k-1）m构成公比为 q的m次幂的等比数列．
已知数列{an}是等差数列，a2=6，a5=12；数列{bn}的前n项和是Sn，且Sn+
1
2
bn=1．
（1）求数列{an}和{bn}通项公式；
（2）记cn=
-2
an•log
bn
2
，数列{cn}的前n项和为Tn，若Tn＜
m-2012
2
对一切n∈N*都成立，求最小正整数m．
若函数f（x）=ax3+3x2-x恰好有三个单调区间，那么a的取值范围是
 
．
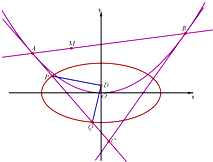已知抛物线C2：x2=2py（p＞0）的通径长为4，椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，且过抛物线C2的焦点．
（1）求抛物线C2和椭圆C1的方程；
（2）过定点M（-1，
3
2
）引直线l交抛物线C2于A，B两点（点A在点B的左侧），分别过A、B作抛物线C2的切线l1，l2，且l1与椭圆C1相交于P，Q两点．记此时两切线l1，l2的交点为点C．
①求点C的轨迹方程；
②设点D（0，
1
4
），求△DPQ的面积的最大值，并求出此时点C的坐标．
若函数f（x）=asinx+cosx的图象关于点（-
π
3
，0）成中心对称，则a=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网