题目内容
已知直线l与抛物线x2=4y相交于A,B两点,且与圆(y-1)2+x2=1相切.
(Ⅰ)求直线l在y轴上截距的取值范围;
(Ⅱ)设F是抛物线的焦点,且
•
=0,求直线l的方程.
(Ⅰ)求直线l在y轴上截距的取值范围;
(Ⅱ)设F是抛物线的焦点,且
| FA |
| FB |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设直线l的方程为y=kx+b.由直线l与圆(y-1)2+x2=1相切,得
=1,化简得k2=b2-2b,直线l的方程代入x2=4y,消去y,由直线l与抛物线x2=4y相交于A,B两点,得△>0,即可求直线l在y轴上截距的取值范围;
(Ⅱ)以
•
=x1x2+(y1-1)(y2-1)+y1y2,结合韦达定理,即可求直线l的方程.
| |b-1| | ||
|
(Ⅱ)以
| FA |
| FB |
解答:
解:(Ⅰ)设直线l的方程为y=kx+b.由直线l与圆(y-1)2+x2=1相切,
得
=1,化简得k2=b2-2b.(2分)
直线l的方程代入x2=4y,消去y,得x2-4kx-4b=0.(*) (3分)
由直线l与抛物线x2=4y相交于A,B两点,得△=(-4k)2+16b>0,即k2+b>0.
将k2=b2-2b代入上式,得b2-b>0.
解得b>1,或b<0.(5分)
注意到k2=b2-2b≥0,从而有b≥2,或b<0.(6分)
(Ⅱ)设A(x1,y1),B(x2,y2).
由(*)得x1+x2=4k,x1x2=-4b.
所以
•
=x1x2+(y1-1)(y2-1)+y1y2=
x1x2+
(x1x2)2-
(x1+x2)2+1.(10分)
将x1+x2=4k,x1x2=-4b代入上式,令
•
=0,得b2-4k2-6b+1=0.
所以b2-4(b2-2b)-6b+1=0,即3b2-2b-1=0.
解得b=-
,b=1(舍去).
故k=±
.
所以直线l的方程为
x+3y+1=0,或
x-3y-1=0.(13分)
得
| |b-1| | ||
|
直线l的方程代入x2=4y,消去y,得x2-4kx-4b=0.(*) (3分)
由直线l与抛物线x2=4y相交于A,B两点,得△=(-4k)2+16b>0,即k2+b>0.
将k2=b2-2b代入上式,得b2-b>0.
解得b>1,或b<0.(5分)
注意到k2=b2-2b≥0,从而有b≥2,或b<0.(6分)
(Ⅱ)设A(x1,y1),B(x2,y2).
由(*)得x1+x2=4k,x1x2=-4b.
所以
| FA |
| FB |
| 3 |
| 2 |
| 1 |
| 16 |
| 1 |
| 4 |
将x1+x2=4k,x1x2=-4b代入上式,令
| FA |
| FB |
所以b2-4(b2-2b)-6b+1=0,即3b2-2b-1=0.
解得b=-
| 1 |
| 3 |
故k=±
| ||
| 3 |
所以直线l的方程为
| 7 |
| 7 |
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
相关题目
下列函数中既是奇函数,又在区间[-1,1]上单调递减的函数是( )
| A、f(x)=|tan2x| | ||||||
| B、f(x)=-|x+1| | ||||||
C、f(x)=
| ||||||
D、f(x)=log
|
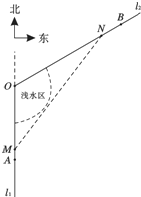 某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.
某港湾的平面示意图如图所示,O,A,B分别是海岸线l1,l2上的三个集镇,A位于O的正南方向6km处,B位于O的北偏东60°方向10km处.