题目内容
2.某几何体的三视图(单位:cm)如图,则这个几何体的表面积为(单位:cm2)( )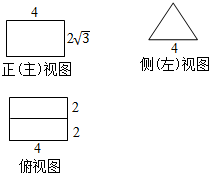
| A. | 24+4$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 24+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
分析 几何体为侧放的直三棱柱,棱柱的底面为侧视图三角形,棱柱的高为4.
解答 解:由三视图可知几何体为侧放的直三棱柱,棱柱的底面为侧视图中的等边三角形,棱柱的高为4.
∴棱柱的表面积S=$\frac{1}{2}×4×2\sqrt{3}×2$+3×4×4=48+8$\sqrt{3}$.
故选B.
点评 本题考查了棱柱的三视图,表面积计算,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.在数列{an}中,a1=1,an+1=2an,Sn为{an}的前n项和,则S5=( )
| A. | -30 | B. | 31 | C. | -32 | D. | 33 |
13.设p:y=cx是R上的单调递减函数;q:函数g(x)=lg(2cx2+2x+1)的值域为R.如果“p且q”为假命题,“p或q”为真命题,则正实数c的取值范围是( )
| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | $({0,\frac{1}{2}})$ |
17.下列叙述中正确的是( )
| A. | “m=2”是“l1:2x+(m+1)y+4=0与l2:mx+3y-2=0平行”的充分条件 | |
| B. | “方程Ax2+By2=1表示椭圆”的充要条件是“A≠B” | |
| C. | 命题“?x∈R,x2≥0”的否定是“?x0∈R,x02≥0” | |
| D. | 命题“a、b都是偶数,则a+b是偶数”的逆否命题为“a+b不是偶数,则a、b都是奇数” |
7.设函数f(x)=$\left\{\begin{array}{l}{{2}^{1-x},x≤1}\\{1-lo{g}_{2}x,x>1}\end{array}\right.$,则不等式f(x)≤2的解集为( )
| A. | (0,1]∪(2,+∞) | B. | [0,+∞) | C. | [0,1] | D. | (0,+∞) |
14.若关于x的方程x3-3x-m=0在[0,2]上有根,则实数m的取值范围是( )
| A. | [-2,2] | B. | [0,2] | C. | [-2,0] | D. | (-∞,-2)∪(2,+∞) |
11.下列说法不正确的是( )
| A. | a∥b,a?α,b⊆α⇒a∥α | B. | α∥β,b∥β,a,b⊆α⇒α∥β | ||
| C. | a⊥b,a⊥c,b∩c=p,p∈α,a?α⇒a⊥α | D. | α⊥β,α∩β=l,b⊆α,b⊥l⇒b⊥β |