题目内容
10.若函数f(x)是定义域为R,最小正周期为π的函数,且当x∈[0,π]时,当f(x)=sinx,则$f(\frac{15π}{4})$=$\frac{\sqrt{2}}{2}$.分析 由题意可得f($\frac{15π}{4}$)=f($\frac{3π}{4}$)=sin$\frac{3π}{4}$,从而求得它的值.
解答 解:由题意可得f($\frac{15π}{4}$)=f($\frac{15π}{4}$-3π)=f($\frac{3π}{4}$),
∵当x∈[0,π]时,f(x)=sinx,∴f($\frac{3π}{4}$)=sin$\frac{3π}{4}$=$\frac{\sqrt{2}}{2}$,
则$f(\frac{15π}{4})$=f($\frac{3π}{4}$)=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{{\sqrt{2}}}{2}$.
点评 本题主要考查函数的周期性的应用,属于基础题.

练习册系列答案
相关题目
20.某一简单几何体的三视图如所示,该几何体的外接球的表面积是( )


| A. | 13π | B. | 16π | C. | 25π | D. | 27π |
1. 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
5.已知点A(2,0),B(0,-1),点P是圆x2+(y-1)2=1上的任意一点,则△PAB面积的最大值为( )
| A. | 2 | B. | $4+\sqrt{5}$ | C. | $1+\frac{{\sqrt{5}}}{2}$ | D. | $2+\frac{{\sqrt{5}}}{2}$ |
15.已知不同的直线m、n,不同的平面α、β,下列四个命题中正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | C. | 若m∥n,n?α,则m∥α | D. | 若m⊥α,n⊥α,则m∥n |
2.某几何体的三视图(单位:cm)如图,则这个几何体的表面积为(单位:cm2)( )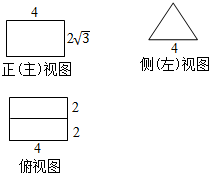

| A. | 24+4$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 24+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
20.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,若函数y=x(f(x)-2)+b有零点,则实数b的取值范围是( )
| A. | (0,1) | B. | (-∞,1] | C. | (2,3) | D. | [2,+∞) |