题目内容
11.下列说法不正确的是( )| A. | a∥b,a?α,b⊆α⇒a∥α | B. | α∥β,b∥β,a,b⊆α⇒α∥β | ||
| C. | a⊥b,a⊥c,b∩c=p,p∈α,a?α⇒a⊥α | D. | α⊥β,α∩β=l,b⊆α,b⊥l⇒b⊥β |
分析 由线面平行判定定理得A正确;在B中,α与β相交或平行;由线面垂直的判定定理得C正确;由面面垂直的性质定理得D正确.
解答 解:在A中,a∥b,a?α,b⊆α⇒a∥α,由线面平行判定定理得A正确;
在B中,α∥β,b∥β,a,b⊆α⇒α与β相交或平行,故B错误;
在C中,a⊥b,a⊥c,b∩c=p,p∈α,a?α⇒a⊥α,由线面垂直的判定定理得C正确;
在D中,α⊥β,α∩β=l,b⊆α,b⊥l⇒b⊥β,由面面垂直的性质定理得D正确.
故选:B.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
1. 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
2.某几何体的三视图(单位:cm)如图,则这个几何体的表面积为(单位:cm2)( )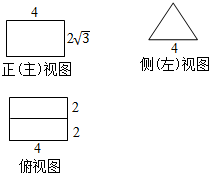

| A. | 24+4$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 24+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
6.棱长为1的正四面体的外接球的半径为( )
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{3}}}{4}$ | C. | 1 | D. | $\frac{{\sqrt{3}}}{3}$ |
16.设x0是方程log2x+x=0的根,则x0属于区间( )
| A. | (0,$\frac{1}{8}$) | B. | ($\frac{1}{8}$,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,$\frac{1}{2}$) | D. | ($\frac{1}{2}$,1) |
20.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,若函数y=x(f(x)-2)+b有零点,则实数b的取值范围是( )
| A. | (0,1) | B. | (-∞,1] | C. | (2,3) | D. | [2,+∞) |