题目内容
13.设p:y=cx是R上的单调递减函数;q:函数g(x)=lg(2cx2+2x+1)的值域为R.如果“p且q”为假命题,“p或q”为真命题,则正实数c的取值范围是( )| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | $({0,\frac{1}{2}})$ |
分析 分别求出两个命题的为真命题的等价条件,利用复合命题真假之间的关系进行判断求解.
解答 解:若y=cx是R上的单调递减函数,则0<c<1,
若函数g(x)=lg(2cx2+2x+1)的值域为R,
则当c=0时,g(x)=lg(2x+1)的值域为R满足条件,
若c≠0,要使函数g(x)=lg(2cx2+2x+1)的值域为R,
则$\left\{\begin{array}{l}{c>0}\\{△=4-8c≥0}\end{array}\right.$,即0<c≤$\frac{1}{2}$,综上$0≤c≤\frac{1}{2}$;
若“p且q”为假命题,“p或q”为真命题,
则p,q为一真一假,
若p真q假,则$\left\{\begin{array}{l}{0<c<1}\\{c>\frac{1}{2}或c<0}\end{array}\right.$,得$\frac{1}{2}$<m<1,
若p假q真,则$\left\{\begin{array}{l}{0<c≤\frac{1}{2}}\\{c≥1或c≤0}\end{array}\right.$,此时无解,
综上正实数c的取值范围是$\frac{1}{2}$<m<1,
故选:A
点评 本题主要考查复合命题真假的应用,根据条件求出两个命题的为真命题的等价条件是解决本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.方程x2+3ax+3a+1=0(a>2)的两根为tanα,tanβ,且α,β∈(-$\frac{π}{2}$,$\frac{π}{2}$),则α+β=( )
| A. | $\frac{π}{4}$ | B. | -$\frac{3π}{4}$ | C. | $\frac{5π}{4}$ | D. | $\frac{π}{4}$或-$\frac{3π}{4}$ |
1. 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
 如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )
如图为某几何体的三视图,该几何体的体积记为V1,将俯视图绕其直径所在的直线旋转一周而形成的曲面所围成的几何体的体积记为V2,则$\frac{{V}_{1}}{{V}_{2}}$=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
8.某大学志愿者协会有10名同学,成员构成如下表,其中表中部分数据不清楚,只知道从这10名同学中随机抽取一位,抽到该名同学为“数学专业”的概率为$\frac{2}{5}$.
(1)求m,n的值;
(2)现从男同学中随机选取2名同学,进行社会公益活动(每位同学被选到的可能性相同),求选出的这2名男同学中至少有一位同学是“数学专业”的概率.
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | n | 1 | m | 1 |
| 女 | 1 | 1 | 1 | 1 |
(2)现从男同学中随机选取2名同学,进行社会公益活动(每位同学被选到的可能性相同),求选出的这2名男同学中至少有一位同学是“数学专业”的概率.
5.已知点A(2,0),B(0,-1),点P是圆x2+(y-1)2=1上的任意一点,则△PAB面积的最大值为( )
| A. | 2 | B. | $4+\sqrt{5}$ | C. | $1+\frac{{\sqrt{5}}}{2}$ | D. | $2+\frac{{\sqrt{5}}}{2}$ |
2.某几何体的三视图(单位:cm)如图,则这个几何体的表面积为(单位:cm2)( )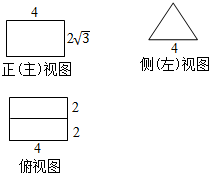

| A. | 24+4$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 24+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |