题目内容
12.下列有关命题的说法错误的个数是( )①命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1”
②“x=-1”是“x2-5x-6=0”的充分不必要条件
③命题“存在x∈R,使得x2+x-1<0”的否定是:“任意x∈R,均有x2+x-1>0”
④命题“若x=y,则sin x=sin y”的逆否命题为真命题
⑤若“p或q”为真命题,则p、q均为真命题.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 ①根据否命题的定义进行判断
②根据充分条件和必要条件的定义进行判断
③根据含有量词的命题的否定进行判断
④根据逆否命题的定义进行判断
⑤根据复合命题之间的关系进行判断.
解答 解:①命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1”,故①错误,
②由x2-5x-6=0得x=-1或x=6,
则“x=-1”是“x2-5x-6=0”的充分不必要条件,故②正确,
③命题“存在x∈R,使得x2+x-1<0”的否定是:“任意x∈R,均有x2+x-1≥0”,故③错误,
④“若x=y,则sin x=sin y”成立,则原命题为真命题.,则原命题的逆否命题为真命题,故④正确,
⑤若“p或q”为真命题,则p、q至少有一个为真命题.故⑤错误,
故错误的命题是①③⑤,共有3个,
故选:B
点评 本题主要考查命题的真假判断,涉及四种命题之间的关系,充分条件和必要条件的判断以及含有量词的命题的否定,复合命题的真假关系,涉及的知识点较多,难度不大.

练习册系列答案
相关题目
2.某几何体的三视图(单位:cm)如图,则这个几何体的表面积为(单位:cm2)( )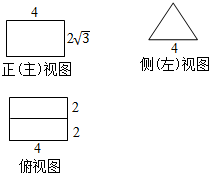

| A. | 24+4$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 24+8$\sqrt{3}$ | D. | 48+4$\sqrt{3}$ |
20.设定义域为(0,+∞)的单调函数f(x),对任意的x∈(0,+∞),都有f[f(x)-lnx]=1,若函数y=x(f(x)-2)+b有零点,则实数b的取值范围是( )
| A. | (0,1) | B. | (-∞,1] | C. | (2,3) | D. | [2,+∞) |