题目内容

7．设函数f（x）=$\left\{\begin{array}{l}{{2}^{1-x}，x≤1}\\{1-lo{g}_{2}x，x＞1}\end{array}\right.$，则不等式f（x）≤2的解集为（　　）
A．（0，1]∪（2，+∞）B．[0，+∞）C．[0，1]D．（0，+∞）

分析 分x≤1和x＞1两种情况列出不等式解出．

解答 解：（1）当x≤1时，21-x≤2，解得x≥0，∴0≤x≤1．
（2）当x＞1时，1-log2x≤2，解得x≥$\frac{1}{2}$，∴x＞1．
综上，不等式f（x）≤2的解集是[0，1]∪（1，+∞）=[0，+∞）．
故选B．

点评 本题考查了分段函数的应用，对数不等式的解法，分类讨论思想，属于中档题．

练习册系列答案
相关题目
17．在△ABC中，a=2$\sqrt{3}$，c=2$\sqrt{2}$，A=60°，则C=（　　）
A．30°B．45°C．45°或135°D．60°
18．已知函数f（x）=4-log2x，g（x）=log2x．
（1）当$x∈（\frac{1}{2}，8）$时，求函数h（x）=f（x）•g（x）的值域；
（2）若对任意的x∈[1，8]，不等式f（x3）•f（x2）＞kg（x）恒成立，求实数k的取值范围．
15．已知不同的直线m、n，不同的平面α、β，下列四个命题中正确的是（　　）
A．若m∥α，n∥α，则m∥nB．若m∥α，m∥β，则α∥βC．若m∥n，n?α，则m∥αD．若m⊥α，n⊥α，则m∥n
2．某几何体的三视图（单位：cm）如图，则这个几何体的表面积为（单位：cm2）（　　）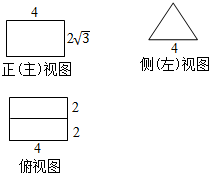
A．24+4$\sqrt{3}$B．48+8$\sqrt{3}$C．24+8$\sqrt{3}$D．48+4$\sqrt{3}$
12．已知函数y=f（x）的定义域为R，对任意的实数x都满足f（x+2）=f（x），当x∈[-1，1]时，f（x）=x2，那么函数y=f（x）的图象与函数y=|lgx|的图象的交点共有（　　）
A．10个B．9个C．8个D．2个
19．下列有关命题的说法正确的是③④．
①|x|≠3⇒x≠3或x≠-3；
②命题“a、b都是偶数，则a+b是偶数”的逆否命题是“a+b不是偶数，则a、b都不是偶数”；
③“|x-1|＜2”是“x＜3”的充分不必要条件
④若一个命题的否命题为真，则它的逆命题一定是真．
16．设x0是方程log2x+x=0的根，则x0属于区间（　　）
A．（0，$\frac{1}{8}$）B．（$\frac{1}{8}$，$\frac{1}{4}$）C．（$\frac{1}{4}$，$\frac{1}{2}$）D．（$\frac{1}{2}$，1）
17．设α和β为不重合的两个平面，给出下列命题：
①若α内的两条相交直线分别平行于β内的两条直线，则α∥β；
②若α外的一条直线l与α内的一条直线平行，则l∥α；
③设α∩β=l，若α内有一条直线垂直于l，则α⊥β；
④若直线l与平面α内的两条直线垂直，则l⊥α．
其中所有的真命题的序号是①②．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网