题目内容
如图所示，平面四边形ABCD中，AB=AD=CD=1，BD=| 2 |
BD⊥CD，将其沿对角线BD折成四面体A-BCD，使平面ABD⊥平面BCD，则下列说法中不正确的是（ ）
| A、平面ACD⊥平面ABD |
| B、AB⊥CD |
| C、平面ABC⊥平面ACD |
| D、AB∥平面ABC |
考点：平面与平面之间的位置关系
专题：空间位置关系与距离
分析：由已知条件推导出CD⊥平面ABD，从而得到平面ACD⊥平面ABD；由已知得AB⊥AD，AB⊥CD，从而AB⊥平面ACD，
进而AB⊥CD；由AB⊥平面ACD，得平面ABC⊥平面ACD；由AB?平面ABC，得AB∥平面ABC不成立．
进而AB⊥CD；由AB⊥平面ACD，得平面ABC⊥平面ACD；由AB?平面ABC，得AB∥平面ABC不成立．
解答：
解：∵BD⊥CD，平面ABD⊥平面BCD，
∴CD⊥平面ABD，
∵CD?平面ACD，
∴平面ACD⊥平面ABD，故A正确；
∵平面四边形ABCD中，AB=AD=CD=1，BD=
，
∴AB⊥AD，
又CD⊥平面ABD，∴AB⊥CD，
又AD∩CD=D，
∴AB⊥平面ACD，
∵CD?平面ACD，∴AB⊥CD，故B正确；
∵AB⊥平面ACD，AB?平面ABC，
∴平面ABC⊥平面ACD，故C正确；
∵AB?平面ABC，∴AB∥平面ABC不成立，故D错误．
故选：D．
∴CD⊥平面ABD，
∵CD?平面ACD，
∴平面ACD⊥平面ABD，故A正确；
∵平面四边形ABCD中，AB=AD=CD=1，BD=
| 2 |
∴AB⊥AD，
又CD⊥平面ABD，∴AB⊥CD，
又AD∩CD=D，
∴AB⊥平面ACD，
∵CD?平面ACD，∴AB⊥CD，故B正确；
∵AB⊥平面ACD，AB?平面ABC，
∴平面ABC⊥平面ACD，故C正确；
∵AB?平面ABC，∴AB∥平面ABC不成立，故D错误．
故选：D．
点评：本题考查命题真假的判断，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
已知f（x）=sinωx（ω＞0）的最小正周期为4π，则f（1），
，
的大小关系为（ ）
| f(2) |
| 2 |
| f(3) |
| 3 |
A、f（1）＞
| ||||
B、
| ||||
C、
| ||||
D、
|
若全集U={-1，-2，-3，-4}，M={-2，-3}，则∁UM（ ）
| A、{-1，-2，-3} |
| B、{-2} |
| C、{-4} |
| D、{-1，-4} |
已知集合M={x|-1≤x≤1，x∈Z}，N={0，1，2}，则M∩N为（ ）
| A、{1} |
| B、{0，1，2} |
| C、{x|0≤x≤1} |
| D、{0，1} |
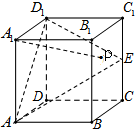如图所示，在长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，AA1=3，E是棱CC1上的点，且