题目内容
已知圆的方程为x2+y2-6x-8y=0．设该圆过点（-1，4）的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积为（ ）
| A、15 | B、30 | C、45 | D、60 |
考点：圆的一般方程
专题：计算题,直线与圆
分析：先把圆的方程化为标准方程，求出圆心和半径，过定点（-1，4）的最长弦是圆的直径，最短弦是过该点与最长弦垂直的直线与圆相交得到的弦．
解答：
解：圆的方程可化为：（x-3）2+（y-4）2=25…①
则圆心O（3，4），半径r=5
AC长为过点（-1，4）和点O的圆的直径d=2×5=10，斜率k=0，
BD为最短弦，所以应与AC垂直为x=-1…②
②代入①得：y2-8y+7=0
解得：x=1或x=7
∴BD=7-1=6，则四边形ABCD面积=
×AC×BD=
×10×6=30．
则圆心O（3，4），半径r=5
AC长为过点（-1，4）和点O的圆的直径d=2×5=10，斜率k=0，
BD为最短弦，所以应与AC垂直为x=-1…②
②代入①得：y2-8y+7=0
解得：x=1或x=7
∴BD=7-1=6，则四边形ABCD面积=
| 1 |
| 2 |
| 1 |
| 2 |
点评：解决本题的关键是结合图形判断最长弦与最短弦的位置．
练习册系列答案
相关题目
已知集合M={x|-1≤x≤1，x∈Z}，N={0，1，2}，则M∩N为（ ）
| A、{1} |
| B、{0，1，2} |
| C、{x|0≤x≤1} |
| D、{0，1} |
已知正方体ABCD-A1B1C1D1的棱长为2a，点E为棱CC1的中点．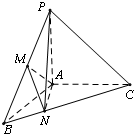
如图，在三棱锥P-ABC中，PA⊥面ABC，∠BAC=120°，且AB=AC=AP，M为PB的中点，N在BC上，且BN=