题目内容

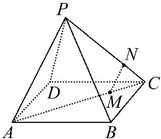如图，四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则（　　）
A、MN∥PD
B、MN∥PA
C、MN∥AD
D、以上均有可能
考点：直线与平面平行的性质
专题：空间位置关系与距离
分析：直接利用直线与平面平行的性质定理推出结果即可．
解答： 解：四棱锥P-ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，
MN?平面PAC，平面PAC∩平面PAD=PA，
由直线与平面平行的性质定理可得：MN∥PA．
故选：B．
点评：本题考查直线与平面平行的性质定理的应用，基本知识的考查．
练习册系列答案
相关题目
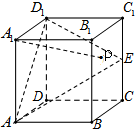如图所示，在长方体ABCD-A1B1C1D1中，底面ABCD是边长为2的正方形，AA1=3，E是棱CC1上的点，且
CE
=
1
3
CC1
，P是侧面BCC1B1上的动点，且A1P∥面D1AE，则A1P与平面BCC1B1所成角的正切值的最大值为（　　）
A、
3
2
B、
10
2
C、
13
2
D、2
设函数f（x）=ax2+bx+c（a，b，c∈R），f（1）=-
a
2
，
（1）若f（x）＜1的解集为（0，3），求f（x）的表达式；
（2）若a＞0，求证：函数f（x）在区间（0，2）内至少有一个零点．
在100件产品中有3件次品，从中任取2件进行检验，至少有1件次品的不同取法有
 
种．
函数y=
5-2sinx
2+sinx
的最大值是
 
．
已知数列{an}为等差数列，Sn是它的前n项和．
（1）若3a5=5a3，求
S1
S5
=
 
．
（2）若{bn}也是等差数列，前n项和Tn且
Sn
Tn
=
2n
3n+1
，求
an
bn
=
 
．
已知函数f（x）=ex-e-x，其中e是自然对数的底数．
（1）证明：f（x）是R上的奇函数；
（2）若函数g（x）=e2x+e-2x-6f（x），求g（x）在区间[0，1]上的最大值．
若方程sin2x+sinx-1-a=0在（0，
π
2
）上有解，则a的取值范围
 
．
若θ为三角形中最大内角，则直线l：xtanθ+y+m=0的倾斜角的范围是（　　）
A、(0，
π
2
)∪(
π
2
，
2π
3
)
B、(
π
3
，
π
2
)∪(
π
2
，
2π
3
)
C、(0，
π
3
)∪(
π
3
，π)
D、(0，
π
2
)∪(
2π
3
，π)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网