题目内容
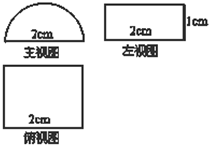 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)
已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)| A、6+2π | B、4+2π |
| C、6+3π | D、4+3π |
考点:由三视图求面积、体积
专题:计算题
分析:由三视图知几何体为半个圆柱,根据三视图的数据求出各个面的面积,再相加.
解答:
解:由三视图知几何体为半个圆柱,圆柱的底面圆直径为2,圆柱的高为2,
∴几何体的表面积=S侧+S底=2×π×1+2×2+2×
×π×12=4+3π.
故选D.
∴几何体的表面积=S侧+S底=2×π×1+2×2+2×
| 1 |
| 2 |
故选D.
点评:本题考查了由三视图求几何体的表面积,解题的关键是判断几何体的形状及相关数据所对应的几何量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积为( )


| A、12-π | B、12-2π |
| C、6-π | D、4-π |
已知函数f(x)=3x2-(k-2)x-8在[5,10]上具有单调性,则实数k的取值范围是( )
| A、[32,62] |
| B、(-∞,32]∪[62,+∞) |
| C、(32,62) |
| D、(-∞,32)∪(62,+∞) |
某几何体的三视图如图所示,则其表面积为( )


| A、8 | ||
| B、2 | ||
C、6+4
| ||
D、4+4
|
实数x,y满足
,则z=x-3y的最小值为( )
|
| A、4 | B、-2 | C、-8 | D、-10 |
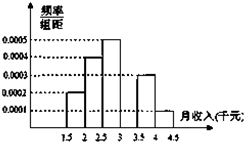 某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是
某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是