题目内容
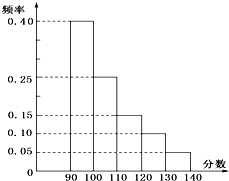某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布图如图所示，若130～140分数段的人数为90人，则90～100分数段的人数为（ ）| A、740 | B、180 |
| C、720 | D、540 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图，先求出样本容量，再求90～100分数段的人数是多少．
解答：
解：根据频率分布直方图，得，
130～140分数段的人数为90人，对应的频率是0.05，
∴样本容量是
=1800；
∴90～100分数段的人数1800×0.40=720．
故选：C．
130～140分数段的人数为90人，对应的频率是0.05，
∴样本容量是
| 90 |
| 0.05 |
∴90～100分数段的人数1800×0.40=720．
故选：C．
点评：本题考查了频率分布直方图的应用问题，解题时应根据频率、频数与样本容量的关系进行解答，是基础题．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
若x=-
是f（x）=cosx+asinx的对称轴，则f（x）=cosx+asinx的初相是（ ）
| π |
| 3 |
A、-
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=-sinx+1的图象大致为（ ）
A、 |
B、 |
C、 |
D、 |
设a∈R，若函数y=ex+3ax（x∈R）有小于零的极值点，则（ ）
| A、-3＜a＜0 | ||
B、-
| ||
| C、a＜-3 | ||
D、a＜-
|
f（x）的定义域为R，f（2+x）=f（2-x），-1＜x＜2时，f（x）=（
）x，则有（ ）
| 1 |
| 2 |
A、f（-
| ||
B、f（4）＜f（1）＜f（-
| ||
C、f（1）＜f（-
| ||
D、f（1）＜f（4）＜f（-
|