题目内容
f(x)的定义域为R,f(2+x)=f(2-x),-1<x<2时,f(x)=(
)x,则有( )
| 1 |
| 2 |
A、f(-
| ||
B、f(4)<f(1)<f(-
| ||
C、f(1)<f(-
| ||
D、f(1)<f(4)<f(-
|
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:先由f(2+x)=f(2-x),求出f(4)=f(0);再根据-1<x<2时,f(x)的单调性判断f(-
)、f(0)、f(1)的大小即可.
| 1 |
| 2 |
解答:
解:根据题意,∵f(2+x)=f(2-x),
∴f(4)=f(2+2)=f(2-2)=f(0);
又∵-1<x<2时,f(x)=(
)x是减函数,
且-
<0<1,
∴f(-
)>f(0)>f(1);
即f(1)<f(4)<f(-
).
故选:D.
∴f(4)=f(2+2)=f(2-2)=f(0);
又∵-1<x<2时,f(x)=(
| 1 |
| 2 |
且-
| 1 |
| 2 |
∴f(-
| 1 |
| 2 |
即f(1)<f(4)<f(-
| 1 |
| 2 |
故选:D.
点评:本题考查了函数的性质与应用问题,解题时应用函数的单调性与对称性进行比较函数值的大小,是基础题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
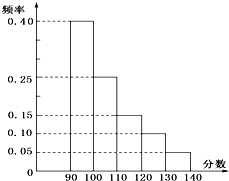 某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为( )
某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为( )| A、740 | B、180 |
| C、720 | D、540 |
已知-1,x,-4成等比数列,则x的值为( )
| A、2 | ||||
B、-
| ||||
| C、2 或-2 | ||||
D、-
|
在等比数列{an}中,a1=2,q=3,则a3=( )
| A、6 | B、8 | C、12 | D、18 |
下列给出的赋值语句中正确的是( )
| A、4=M | B、M=-M |
| C、B=A-3 | D、x+y=0 |
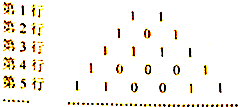 将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是
将二项式系数表中的奇数换成1,偶数换成0,得到如图所示的0-1三角数表,从上往下数,第1次全行的数都为1的是第1行,第二次全行的数都为1的是第3行,…,那么第61行中1的个数是