题目内容
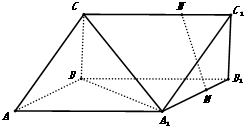 如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证:
如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证:(1)AB⊥A1C;
(2)CN=2NC1.
考点:直线与平面垂直的性质
专题:综合题,空间位置关系与距离
分析:(1)取AB中点E,连结CE,A1B,A1E,证明AB⊥面CEA1,即可证明AB⊥A1C;
(2)在BB1上取点H,使BH=2HB1,连接HN,HM,证明平面MNH∥平面A1BC,可得NH∥BC,再证明四边形BHNC为平行四边形,即可证明CN=2NC1.
(2)在BB1上取点H,使BH=2HB1,连接HN,HM,证明平面MNH∥平面A1BC,可得NH∥BC,再证明四边形BHNC为平行四边形,即可证明CN=2NC1.
解答:
证明: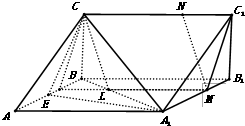 (1)取AB中点E,连结CE,A1B,A1E,
(1)取AB中点E,连结CE,A1B,A1E,
∵AB=AA1,∠BAA1=60°,∴△BAA1=60°是正三角形,
∴A1E⊥AB,
∵CA=CB,∴CE⊥AB,
∵CE∩A1E=E,
∴AB⊥面CEA1,又∵A1C在平面CEA1内
∴AB⊥A1C.…(6分)
(2)在BB1上取点H,使BH=2HB1,连接HN,HM,
则HM∩MN=M,MH不在平面A1BC内.
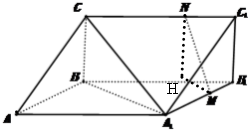
∵A1M=2MB1,∴MH∥A1B.
∴MH∥平面A1BC.…(8分)
又∵MN∥平面A1BC,MN、MH均在平面MNH内,
∴平面MNH∥平面A1BC.…(10分)
∵三棱柱ABC-A1B1C1中,侧面BB1C1C∩平面MNH=NH,
侧面BB1C1C∩平面ABC=BC,
∴NH∥BC.…(12分)
再结合三棱柱ABC-A1B1C1的侧棱CC1∥BB1,可得四边形BHNC为平行四边形,进而BH=CN.
又∵三棱柱ABC-A1B1C1的侧棱CC1=BB1,
∴HB1=NC1.∴CN=2NC1.…(14分)
 (1)取AB中点E,连结CE,A1B,A1E,
(1)取AB中点E,连结CE,A1B,A1E,∵AB=AA1,∠BAA1=60°,∴△BAA1=60°是正三角形,
∴A1E⊥AB,
∵CA=CB,∴CE⊥AB,
∵CE∩A1E=E,
∴AB⊥面CEA1,又∵A1C在平面CEA1内
∴AB⊥A1C.…(6分)
(2)在BB1上取点H,使BH=2HB1,连接HN,HM,
则HM∩MN=M,MH不在平面A1BC内.

∵A1M=2MB1,∴MH∥A1B.
∴MH∥平面A1BC.…(8分)
又∵MN∥平面A1BC,MN、MH均在平面MNH内,
∴平面MNH∥平面A1BC.…(10分)
∵三棱柱ABC-A1B1C1中,侧面BB1C1C∩平面MNH=NH,
侧面BB1C1C∩平面ABC=BC,
∴NH∥BC.…(12分)
再结合三棱柱ABC-A1B1C1的侧棱CC1∥BB1,可得四边形BHNC为平行四边形,进而BH=CN.
又∵三棱柱ABC-A1B1C1的侧棱CC1=BB1,
∴HB1=NC1.∴CN=2NC1.…(14分)
点评:本题考查线面垂直,考查面面平行,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
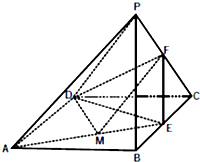 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=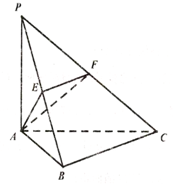 如图,在三棱锥P-ABC中,∠ABC=90°,PA⊥平面ABC,E,F分别为PB,PC的中点.
如图,在三棱锥P-ABC中,∠ABC=90°,PA⊥平面ABC,E,F分别为PB,PC的中点. 在平面直角坐标系xOy中,已知AB是椭圆
在平面直角坐标系xOy中,已知AB是椭圆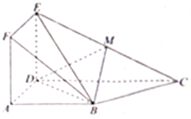 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AD=