题目内容
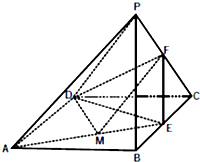 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的菱形,且∠DAB=60°,PA=PD=| 2 |
(Ⅰ)证明:平面ADP⊥平面DEF;
(Ⅱ)在线段AE上是否存在一点M,使二面角M-DF-E的大小为60°,若存在求出EM:MA,若不存在,则说明理由.
考点:与二面角有关的立体几何综合题,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)连结BD,已知条件推导出PB⊥BD,PB⊥AB,从而得到EF⊥平面ABCD,由此能够证明AD⊥面DEF,从而得到平面ADP⊥平面DEF.
(2)以E为原点,CB、CD为x轴、y轴,建立空间直角坐标系E-xyz,利用向量法能求出EM:MA=3:4.
(2)以E为原点,CB、CD为x轴、y轴,建立空间直角坐标系E-xyz,利用向量法能求出EM:MA=3:4.
解答:
(1)证明:连结BD,由题意知△ABD是等边三角形,∴BD=1,
∴BD2+PB2=PD2,∴PB⊥BD,
又∵AB2+PB2=PA2,∴PB⊥AB,且AB∩BD=B,
∴PB⊥平面ABCD,∵PB∥EF,∴EF⊥平面ABCD,∴EF⊥AD,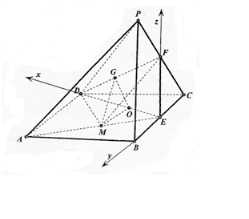
又△BCD是等边三角形,∴BC⊥DE,
∵AD∥BC,∴AD⊥DE,
又DE∩EF=E,∴AD⊥面DEF.
∵AD?平面ADP,∴平面ADP⊥平面DEF.
(2)解:∵EF⊥平面ABCD,
∴以E为原点,CB、CD为x轴、y轴,建立空间直角坐标系E-xyz,
则D(
,0,0),F(0,0,
),A(
,1,0),
=λ
=λ(
,1,0)=(
λ,λ,0),
=(
λ-
,λ,0),
=(-
,0,
),
平面DMF的法向量为
=(λ,
-
λ,
λ),
平面DEF的法向量
=(0,1,0),
由|cos<
,
>|=
,得λ=
,
∴EM:MA=3:4.
∴BD2+PB2=PD2,∴PB⊥BD,
又∵AB2+PB2=PA2,∴PB⊥AB,且AB∩BD=B,
∴PB⊥平面ABCD,∵PB∥EF,∴EF⊥平面ABCD,∴EF⊥AD,

又△BCD是等边三角形,∴BC⊥DE,
∵AD∥BC,∴AD⊥DE,
又DE∩EF=E,∴AD⊥面DEF.
∵AD?平面ADP,∴平面ADP⊥平面DEF.
(2)解:∵EF⊥平面ABCD,
∴以E为原点,CB、CD为x轴、y轴,建立空间直角坐标系E-xyz,
则D(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| EM |
| EA |
| ||
| 2 |
| ||
| 2 |
| DM |
| ||
| 2 |
| ||
| 2 |
| DF |
| ||
| 2 |
| 1 |
| 2 |
平面DMF的法向量为
| n |
| ||
| 2 |
| ||
| 2 |
| 3 |
平面DEF的法向量
| m |
由|cos<
| n |
| m |
| 1 |
| 2 |
| 3 |
| 7 |
∴EM:MA=3:4.
点评:本题考查平面与平面垂直的证明,考查两条线段的比值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
定义在R上的函数f(x)满足f(x)=
,则f(2014)的值是( )
|
| A、-1 |
| B、1 |
| C、log23 |
| D、-log23 |
函数f(x)=(2x-3)ex的单调递增区间是( )
A、(-∞,
| ||
| B、(2,+∞) | ||
C、(0,
| ||
D、(
|
对实数a和b,定义运算“?”:a?b=
,设函数f(x)=x2?(x+2),x∈R,若函数y=f(x)-c的图象与x轴恰有三个公共点,则实数c的取值范围是( )
|
| A、[-1,0) |
| B、(0,1) |
| C、(-1,0) |
| D、(-1,0)∪[1,+∞) |
 如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC.
如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC. 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=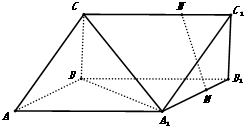 如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证:
如图,三棱柱中ABC-A1B1C1,CA=CB,AB=AA1,∠BAA1=60°,点M和N分别为线段A1B1和CC1上的点,且A1M=2MB1,MN∥平面A1BC.求证: