题目内容
已知实数m,n满足:关于x的不等式|x2+mx+n|≤|3x2-6x-9|的解集为R
(1)求m,n的值;
(2)若a,b,c∈R+,且a+b+c=m-n,求证:
+
+
≤
.
(1)求m,n的值;
(2)若a,b,c∈R+,且a+b+c=m-n,求证:
| a |
| b |
| c |
| 3 |
考点:不等式的证明,绝对值不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:(1)若不等式|x2+mx+n|≤|3x2-6x-9|的解集为R,故3x2-6x-9=0时,x2+mx+n=0,进而由韦达定理得到答案;
(2)运用重要不等式a+b≥2
,结合累加法和三个数的完全平方公式,即可得证.
(2)运用重要不等式a+b≥2
| ab |
解答:
(1)解:∵不等式|x2+mx+n|≤|3x2-6x-9|的解集为R,
令3x2-6x-9=0,得x=-1,或x=3,
故x=-1,或x=3时,x2+mx+n=0,
则x=-1和x=3为方程x2+mx+n=0的两根,
故-1+3=2=-m,-1×3=-3=n,
解得:m=-2,n=-3,
当m=-2,n=-3时,不等式|x2+mx+n|≤|3x2-6x-9|即为
|x2-2x-3|≤3|x2-2x-3|,即有|x2-2x-3|≥0,则解集为R,
故m=-2,n=-3;
(2)证明:若a,b,c∈R+,且a+b+c=m-n=1,
由a+b≥2
,b+c≥2
,c+a≥2
.
累加得,2a+2b+2c≥2
+2
+2
,
两边同时加a+b+c,可得
3(a+b+c)≥a+b+c+2
+2
+2
,
即有3(a+b+c)≥(
+
+
)2,
即
+
+
≤
=
.(当且仅当a=b=c时取得等号)
则
+
+
≤
成立.
令3x2-6x-9=0,得x=-1,或x=3,
故x=-1,或x=3时,x2+mx+n=0,
则x=-1和x=3为方程x2+mx+n=0的两根,
故-1+3=2=-m,-1×3=-3=n,
解得:m=-2,n=-3,
当m=-2,n=-3时,不等式|x2+mx+n|≤|3x2-6x-9|即为
|x2-2x-3|≤3|x2-2x-3|,即有|x2-2x-3|≥0,则解集为R,
故m=-2,n=-3;
(2)证明:若a,b,c∈R+,且a+b+c=m-n=1,
由a+b≥2
| ab |
| bc |
| ca |
累加得,2a+2b+2c≥2
| ab |
| bc |
| ca |
两边同时加a+b+c,可得
3(a+b+c)≥a+b+c+2
| ab |
| bc |
| ca |
即有3(a+b+c)≥(
| a |
| b |
| c |
即
| a |
| b |
| c |
| 3(a+b+c) |
| 3 |
则
| a |
| b |
| c |
| 3 |
点评:本题考查不等式的解法和运用,主要考查不等式的恒成立转化为求函数的最值,同时考查二次方程的韦达定理的运用,运用均值不等式和累加法是证明不等式的关键.

练习册系列答案
相关题目
下列关系式,正确的是( )
A、(
| ||||||
B、log
| ||||||
| C、0.52.3>0.62.3 | ||||||
| D、log34<log0.30.4 |
已知集合A={x|x2≥1},B={x|y=
},则A∩∁RB=( )
| 1-log2x |
| A、(2,+∞) |
| B、(-∞,-1]∪(2,+∞) |
| C、(-∞,-1)∪(2,+∞) |
| D、[-1,0]∪[2,+∞) |
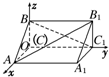 如图所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为
如图所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为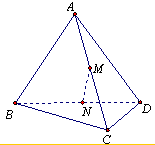 已知空间四边形ABCD中,AB⊥CD,AB=4,CD=4
已知空间四边形ABCD中,AB⊥CD,AB=4,CD=4