Question

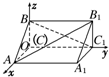如图所示，在空间直角坐标系中有直三棱柱ABCA₁B₁C₁，CA=CC₁=2CB，则直线BC₁与直线AB₁夹角的余弦值为

 

．

Answer 1

考点：异面直线及其所成的角

专题：空间角

分析：不妨令CB=1，则CA=CC₁=2．由cos＜

BC1

，

AB1

＞=

| BC1 • AB1 |

| BC1 |•| AB1 |

，能求出直线BC₁与直线AB₁夹角的余弦值．

解答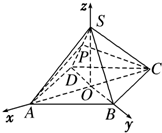： 解：不妨令CB=1，则CA=CC₁=2．
可得O（0，0，0），B（0，0，1），C₁（0，2，0），
A（2，0，0），B₁（0，2，1），
∴

BC1

=（0，2，-1），

AB1

=（-2，2，1），
∴cos＜

BC1

，

AB1

＞=

| BC1 • AB1 |

| BC1 |•| AB1 |

=

4-1

5 × 9

=

1

5

=

5

5

＞0．
∴

BC1

与

AB1

的夹角即为直线BC₁与直线AB₁的夹角，
∴直线BC₁与直线AB₁夹角的余弦值为

5

5

．

点评：本题考查异面直线所成角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．