题目内容
13.已知函数f(x)=x3-ax2-3x.(1)若f(x)在[1,+∞)上是增函数,求实数a的取值范围.
(2)若x=3是f(x)的极值点,求f(x)的单调区间及极值.
分析 (1)对函数f(x)=x3-ax2-3x进行求导,转化成f′(x)在[1,+∞)上恒有f′(x)≥0,求出参数a的取值范围.
(2)先求导,再根据f′(3)=0,求得a=5,再根据导数求出函数极值即可.
解答 解:(1)f′(x)=3x2-2ax-3,
∵f(x)在[1,+∞)上是增函数,
∴f′(x)在[1,+∞)上恒有f′(x)≥0,
即3x2-2ax-3≥0在[1,+∞)上恒成立.
则必有$\frac{a}{3}$≤1且f′(1)=-2a≥0,
∴a≤0;
实数a的取值范围是(-∞,0].
(2)∵f(x)=x3-ax2+3x.
∴f′(x)=3x2-2ax+3.
由题意有f′(3)=0,解得a=5,
故f(x)=x3-5x2+3x,
∴f′(x)=3x2-10x+3=(3x-1)(x-3)
令 f′(x)>0,解得:x>3或x<$\frac{1}{3}$,
令f′(x)<0,解得:$\frac{1}{3}$<x<3,
故f(x)在(-∞,$\frac{1}{3}$)递增,在($\frac{1}{3}$,3)递减,在(3,+∞)递增,
故f(x)极大值=f($\frac{1}{3}$)=$\frac{13}{27}$,f(x)极小值=f(3)=-9.
点评 本题考查函数与导函数的关系,函数的单调性与导数的关系,通过函数的导数求解函数极值,考查转化思想与计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
3.已知线性相关的两个变量之间的几组数据如表:
且回归方程为$\widehat{y}$=kx+35,经预测x=5时,$\widehat{y}$的值为60,则m=( )
| 变量x | 2.7 | 2.9 | 3 | 3.2 | 4.2 |
| 变量y | 46 | 49 | m | 53 | 55 |
| A. | 50 | B. | 51 | C. | 52 | D. | 53 |
18.复数z=$\frac{2-i}{1+i}$(其中i是虚数单位)的虚部为( )
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
5.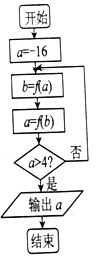 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
 在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )
在如图所示的程序框图中,若函数f(x)=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}(-x)(x<0)}\\{{2}^{x}(x≥0)}\end{array}\right.$,则输出的结果是( )| A. | 16 | B. | 8 | C. | 216 | D. | 28 |
2.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机有放回的抽取2张,则取出的2张卡片上的数字之差的绝对值为奇数的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |