题目内容
8.若点P在曲线y=x3-x+1上移动,设点P处的切线的倾斜角为α,则α的取值范围是[0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π).分析 求函数的导数,利用导数的几何意义,结合正切函数的图象和性质即可得到结论.
解答 解:∵y=x3-x+1,
∴y′=3x2-1≥-1,
∴tanα≥-1,
过P点的切线的倾斜角的取值范围是α∈[0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π),
故答案为:[0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π).
点评 本题主要考查导数的几何意义以及正切函数的图象和性质,综合性较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若sinx+cosx=$\frac{1}{5}$,0<x<π,则tanx的值是( )
| A. | $\frac{4}{3}或-\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}或-\frac{3}{4}$ |
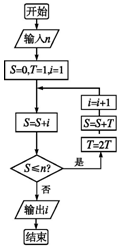 执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.
执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.