题目内容
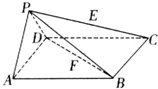 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
| ||
| 2 |
(Ⅰ)求证:EF∥平面PAD;
(Ⅱ)求三棱锥F-DEC的体积;
(Ⅲ)在线段AB上是否存在一点G,使得平面EFG⊥平面PDC?若存在,请说明其位置,并加以证明;若不存在,请说明理由.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(I)连接AC交BD于F,利用三角形的中位线定理即可得到EF∥AP,再利用线面平行的判定定理即可证明;
(II)取AD的中点O,连接OP.由等腰三角形的性质可得PO⊥AD,再利用面面垂直的性质可得PO⊥底面ABCD,计算出三棱锥F-DEC的高,利用三棱锥的体积计算公式即可得出;
(III)设点G为AB中点满足条件,利用三角形的中位线定理可证明FG∥AD,再利用(I)的结论和面面平行的判定定理即可证明平面EFG∥平面PAD.利用面面垂直的性质可证明CD⊥平面PAD.再利用面面垂直的性质定理即可得到结论.
(II)取AD的中点O,连接OP.由等腰三角形的性质可得PO⊥AD,再利用面面垂直的性质可得PO⊥底面ABCD,计算出三棱锥F-DEC的高,利用三棱锥的体积计算公式即可得出;
(III)设点G为AB中点满足条件,利用三角形的中位线定理可证明FG∥AD,再利用(I)的结论和面面平行的判定定理即可证明平面EFG∥平面PAD.利用面面垂直的性质可证明CD⊥平面PAD.再利用面面垂直的性质定理即可得到结论.
解答:
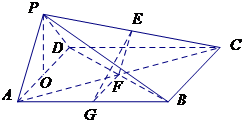 (Ⅰ)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,
(Ⅰ)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,
∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(Ⅱ)解:如图,取AD的中点O,连接OP.
∵PA=AD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PO⊥平面ABCD.
∵E为PC的中点,
∴三棱锥F-DEC的高为h=
PO,
∵PA=PD=
AD,且AD=a,
∴PO=
,
∴h=
,
∴三棱锥F-DEC的体积是VE-FDC=
S△FDCh=
•
a•
a•
a=
a3;
(Ⅲ)解:存在点G满足条件,证明如下:
设点G为AB中点,连接EG、FG.
由F为BD的中点,∴FG∥AD,
由(I)得EF∥PA,且FG∩EF=F,AD∩PA=A,
∴平面EFG∥平面PAD.
∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,AD⊥CD,
∴CD⊥平面PAD.
∴CD⊥平面EFG.
∵CD?平面PDC,
∴平面PDC⊥平面EFG.
AB的中点G为满足条件的点.
 (Ⅰ)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,
(Ⅰ)证明:连接AC,则F是AC的中点,在△CPA中,EF∥PA,∵PA?平面PAD,EF?平面PAD,
∴EF∥平面PAD;
(Ⅱ)解:如图,取AD的中点O,连接OP.
∵PA=AD,∴PO⊥AD.
∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PO⊥平面ABCD.
∵E为PC的中点,
∴三棱锥F-DEC的高为h=
| 1 |
| 2 |
∵PA=PD=
| ||
| 2 |
∴PO=
| a |
| 2 |
∴h=
| a |
| 4 |
∴三棱锥F-DEC的体积是VE-FDC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 48 |
(Ⅲ)解:存在点G满足条件,证明如下:
设点G为AB中点,连接EG、FG.
由F为BD的中点,∴FG∥AD,
由(I)得EF∥PA,且FG∩EF=F,AD∩PA=A,
∴平面EFG∥平面PAD.
∵侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,AD⊥CD,
∴CD⊥平面PAD.
∴CD⊥平面EFG.
∵CD?平面PDC,
∴平面PDC⊥平面EFG.
AB的中点G为满足条件的点.
点评:熟练掌握三角形的中位线定理、线面平行的判定定理、等腰三角形的性质、面面垂直的性质、三棱锥的体积计算公式、面面平行的判定和性质定理、面面垂直的性质是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 一个几何体的三视图如图所示,则该几何体的体积是( )
一个几何体的三视图如图所示,则该几何体的体积是( )| A、π | B、2π | C、3π | D、4π |