题目内容
已知等比数列{an}的前n项和为Sn，a4=2a3，S2=6．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足：bn=an+log2an，求数列{bn}的前n项和Tn．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）若数列{bn}满足：bn=an+log2an，求数列{bn}的前n项和Tn．
考点：数列的求和
专题：等差数列与等比数列
分析：（Ⅰ）利用等比数列{an}的通项公式和前n项和公式由已知条件求出首项和公比，由此能求出数列{an}的通项公式．
（Ⅱ）bn=an+log2an=2n+log22n=2n+n，由此利用分组求和法能求出数列{bn}的前n项和Tn．
（Ⅱ）bn=an+log2an=2n+log22n=2n+n，由此利用分组求和法能求出数列{bn}的前n项和Tn．
解答：
解：（Ⅰ）设等比数列{an}的公比为q，
由
，得
…（2分）
解得
…（4分）
所以an=a1qn-1=2n．…（6分）
（Ⅱ）bn=an+log2an=2n+log22n=2n+n，…（8分）
所以Tn=(21+1)+(22+2)+…+(2n+n)
=（21+22+…+2n）+（1+2+…+n）…（9分）
=
+
=2n+1+
-2．…（12分）
由
|
|
解得
|
所以an=a1qn-1=2n．…（6分）
（Ⅱ）bn=an+log2an=2n+log22n=2n+n，…（8分）
所以Tn=(21+1)+(22+2)+…+(2n+n)
=（21+22+…+2n）+（1+2+…+n）…（9分）
=
| 2(1-2n) |
| 1-2 |
| n(n+1) |
| 2 |
=2n+1+
| n(n+1) |
| 2 |
点评：本小题主要考查等差数列、等比数列等基础知识，考查运算求解能力，考查函数与方程思想，注意分组求和法的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
某大学生在开学季准备销售一种文具套盒进行试创业，在一个开学季内，每售出1盒该产品获利润50元，未售出的产品，每盒亏损30元．根据历史资料，得到开学季市场需求量的频率分布直方图，如图所示．该同学为这个开学季购进了160盒该产品，以X（单位：盒，100≤X≤200）表示这个丌学季内的市场需求量，Y（单位：元）表示这个开学季内经销该产品的利润．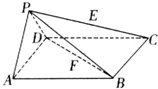
如图所示，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且PA=PD=
