题目内容
设函数f(x)=
sin(2x-
)+2cos2x.
(1)求f(x)的对称轴方程;
(2)设函数g(x)对任意x∈?,都有g(x)=g(x+
),且当x∈[0,
]时,g(x)=f(x)-1,求g(x)在区间[-π,0]上的解析式.
| 2 |
| π |
| 4 |
(1)求f(x)的对称轴方程;
(2)设函数g(x)对任意x∈?,都有g(x)=g(x+
| π |
| 2 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式化简,进而根据三角函数图象与性质求得函数的对称轴返程.
(2)先求得g(x)的表达式,进而对x进行分类讨论,分别求得g(x)的解析式.
(2)先求得g(x)的表达式,进而对x进行分类讨论,分别求得g(x)的解析式.
解答:
解:证明:(1)∵f(x)=
(sin2xcos
-cos2xsin
)+1+cos2x=1+sin2x,
∴由2x=kπ+
,(k∈z)得f(x)的对称轴方程为x=
+
,(k∈z)
(2)当时x∈[0,
]时,g(x)=f(x)-1=1+sin2x-1=sin2x,故
①当x∈[-
,0]时,x+
∈[0,
]…(7分)∵对任意x∈?,都有g(x)=g(x+
)∴g(x)=g(x+
)=sin[2(x+
)]=sin(2x+π)=-sin2x,
②当x∈[-π,-
]时,x+π∈[0,
],从而…(11分)g(x)=g(x+π)=sin[2(x+π)]=sin(2x+2π)=sin2x,
综合①②得:g(x)在区间[-π,0]上的解析式为g(x)=
.
| 2 |
| π |
| 4 |
| π |
| 4 |
∴由2x=kπ+
| π |
| 2 |
| kπ |
| 2 |
| π |
| 4 |
(2)当时x∈[0,
| π |
| 2 |
①当x∈[-
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
②当x∈[-π,-
| π |
| 2 |
| π |
| 2 |
综合①②得:g(x)在区间[-π,0]上的解析式为g(x)=
|
点评:本题主要考查了三角函数恒等变换的应用,三角函数图象与性质.考查了学生分析和推理的能力.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
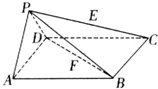 如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
