题目内容
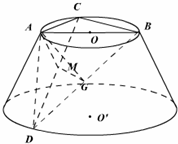如图所示，AB是圆台上底面⊙O的直径，C是⊙O上不同于A、B的一点，D是圆台下底面⊙O′上的一点，过A、B、C、D的截面垂直与底面，M是CD的中点，又AC=AD=2，∠CAD=120°，∠BCD=30°．（1）求证AM⊥平面BCD；
（2）求二面角A-DB-C的正切值．
考点：二面角的平面角及求法,直线与平面垂直的判定
专题：空间角
分析：（Ⅰ）由已知条件推导出BC⊥AC，BC⊥面ACD，从而得到BC⊥AM．由此证明AM⊥平面BCD．
（Ⅱ）作MG⊥BD于G，连接AG，由三垂线定理知∠AGM就是二面角A-DB-C的平面角．由此能求出二面角A-DB-C的正切值．
（Ⅱ）作MG⊥BD于G，连接AG，由三垂线定理知∠AGM就是二面角A-DB-C的平面角．由此能求出二面角A-DB-C的正切值．
解答：
（本小题满分12分）
（Ⅰ）证明：由AB是⊙O的直径，C是⊙O上不同于A、B的一点，
知BC⊥AC．
∵面ACD⊥面ABC，∴BC⊥面ACD，∴BC⊥AM．
∵AC=AD，M是CD的中点，∴AM⊥CD，
∴AM⊥平面BCD．…（6分）
（Ⅱ）作MG⊥BD于G，连接AG．
由（1）知AM⊥平面BCD，根据三垂线定理得AG⊥BD，
∴∠AGM就是二面角A-DB-C的平面角．
∵AC=AD=2，∠CAD=120°，M是CD的中点，∴AM=1，DM=
，
在Rt△MGD中，MG=MDsin∠MDG=
sin30°=
．
∴在Rt△AMG中，tan∠AGM=
=
=
．…（12分）
（Ⅰ）证明：由AB是⊙O的直径，C是⊙O上不同于A、B的一点，
知BC⊥AC．
∵面ACD⊥面ABC，∴BC⊥面ACD，∴BC⊥AM．
∵AC=AD，M是CD的中点，∴AM⊥CD，∴AM⊥平面BCD．…（6分）
（Ⅱ）作MG⊥BD于G，连接AG．
由（1）知AM⊥平面BCD，根据三垂线定理得AG⊥BD，
∴∠AGM就是二面角A-DB-C的平面角．
∵AC=AD=2，∠CAD=120°，M是CD的中点，∴AM=1，DM=
| 3 |
在Rt△MGD中，MG=MDsin∠MDG=
| 3 |
| 3 |
| ||
| 2 |
∴在Rt△AMG中，tan∠AGM=
| AM |
| MG |
| 1 | ||||
|
2
| ||
| 3 |
点评：本题考查直线与平面垂直的证明，考查二面角的正切值的求法，解题时要认真审题，注意空间思维能力的合理运用．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
函数y=sin（2x-
）的单调递减区间是（ ）
| π |
| 4 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|