题目内容
函数y=sin（2x-
）的单调递减区间是（ ）
| π |
| 4 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
考点：正弦函数的单调性
专题：三角函数的图像与性质
分析：根据正弦函数的单调性即可得到结论．
解答：
解：由2kπ+
≤2x-
≤2kπ+
，（k∈Z）解得kπ+
≤x≤kπ+
]（k∈Z），
即函数的单调递减区间为[kπ+
，kπ+
]（k∈Z），
故选：D．
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| 3π |
| 8 |
| 7π |
| 8 |
即函数的单调递减区间为[kπ+
| 3π |
| 8 |
| 7π |
| 8 |
故选：D．
点评：本题主要考查函数单调区间的求解，利用正弦函数的单调性是解决本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知f′（x）是 f（x）的导函数，则
=（ ）
| lim |
| t→0 |
| f(3)-f(3-t) |
| t |
| A、f′（3） |
| B、f′（t） |
| C、-f′（3） |
| D、-f′（t） |
复数z=
（i为虚数单位）在复平面内对应点的坐标是（ ）
| 2+4i |
| 1-i |
| A、（3，3） |
| B、（-1，3） |
| C、（3，-1） |
| D、（2，4） |
一个几何体的三个视图都是矩形，则该几何体可以是（ ）
| A、棱柱 | B、棱台 | C、圆柱 | D、棱锥 |
已知a＞0，b＞0，且H=max{
，
}，其中maxA表示数集A中的最大数．则下列结论中正确的是（ ）
| 1 |
| a |
| a2+b2 |
| b |
A、H有最大值
| ||||
B、H有最小值
| ||||
C、H有最小值
| ||||
D、H有最大值
|
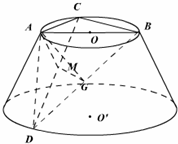如图所示，AB是圆台上底面⊙O的直径，C是⊙O上不同于A、B的一点，D是圆台下底面⊙O′上的一点，过A、B、C、D的截面垂直与底面，M是CD的中点，又AC=AD=2，∠CAD=120°，∠BCD=30°．