题目内容
已知椭圆C的中心在原点,焦点在x轴上,其离心率e=
,短轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点Q(1,1),直线l:y=x+m(m∈R)和椭圆C相交于A、B两点,是否存在实数m,使△ABQ的面积S最大?若存在,求出m的值;若不存在,说明理由.
| ||
| 3 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)已知点Q(1,1),直线l:y=x+m(m∈R)和椭圆C相交于A、B两点,是否存在实数m,使△ABQ的面积S最大?若存在,求出m的值;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意可设椭圆C的方程为
+
=1,(a>b>0),又e=
=
,2b=4,由此能求出椭圆C的方程.
(Ⅱ)设直线l:y=x+m.m∈R和椭圆C相交于A(x1,y1)、B(x2,y2)两点.联立方程
,得13x2+18mx+9m2-36=0.由此利用根的判别式和韦达定理结合已知条件能求出当m=±
时,S取得最大值3.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 3 |
(Ⅱ)设直线l:y=x+m.m∈R和椭圆C相交于A(x1,y1)、B(x2,y2)两点.联立方程
|
| ||
| 2 |
解答:
解:(Ⅰ)由题意可设椭圆C的方程为
+
=1,(a>b>0),
又e=
=
,2b=4,a2=b2+c2,解得a=3,b=2.
故椭圆C的方程为
+
=1.
(Ⅱ)设直线l:y=x+m.m∈R和椭圆C相交于A(x1,y1)、B(x2,y2)两点.
联立方程得,
,消去y得,13x2+18mx+9m2-36=0.
上式有两个不同的实数根,
△=324m2-4×13×9(m2-4)=144(13-m2)>0.
且x1+x2=-
,x1x2=
.
∴AB=
=
=
×
.
点Q(1,1)到l:y=x+m的距离为
.
∴△ABQ的面积S=
×
×
×
=
×
≤
×
=3.
当且仅当13-m2=m2,即m=±
时,S取得最大值,最大值为3.
| x2 |
| a2 |
| y2 |
| b2 |
又e=
| c |
| a |
| ||
| 3 |
故椭圆C的方程为
| x2 |
| 9 |
| y2 |
| 4 |
(Ⅱ)设直线l:y=x+m.m∈R和椭圆C相交于A(x1,y1)、B(x2,y2)两点.
联立方程得,
|
上式有两个不同的实数根,
△=324m2-4×13×9(m2-4)=144(13-m2)>0.
且x1+x2=-
| 18m |
| 13 |
| 9m2-36 |
| 13 |
∴AB=
| (x1-x2)2+(y1-y2)2 |
| 2[(x1+x2)2-4x1x2] |
12
| ||
| 13 |
| 13-m2 |
点Q(1,1)到l:y=x+m的距离为
| |m| | ||
|
∴△ABQ的面积S=
| 1 |
| 2 |
12
| ||
| 13 |
| 13-m2 |
| |m| | ||
|
=
| 6 |
| 13 |
| (13-m2)m2 |
| 6 |
| 13 |
| 13-m2+m2 |
| 2 |
当且仅当13-m2=m2,即m=±
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查三角形面积的最大值是否存在的判断,解题时要认真审题,注意根的判别式和韦达定理的合理运用.

练习册系列答案
相关题目
已知a>0,b>0,且H=max{
,
},其中maxA表示数集A中的最大数.则下列结论中正确的是( )
| 1 |
| a |
| a2+b2 |
| b |
A、H有最大值
| ||||
B、H有最小值
| ||||
C、H有最小值
| ||||
D、H有最大值
|
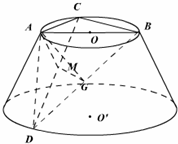 如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.
如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.
