题目内容
在无穷数列{an}中,a1=1,对于任意n∈N*,都有an∈N*,an<an+1.设m∈N*,记使得an≤m成立的n最大值为bm.
(Ⅰ)设数列为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{bn}为等差数列,求出所有可能的数列{an};
(Ⅲ)设ap=q,a1+a2+…+ap=A,求b1+b2+…+bq的值.(用p,q,A表示)
(Ⅰ)设数列为1,3,5,7,…,写出b1,b2,b3的值;
(Ⅱ)若{bn}为等差数列,求出所有可能的数列{an};
(Ⅲ)设ap=q,a1+a2+…+ap=A,求b1+b2+…+bq的值.(用p,q,A表示)
考点:数列的求和
专题:规律型,等差数列与等比数列
分析:(Ⅰ)根据使得an≤m成立的n的最大值为bm,即可写出b1,b2,b3的值;
(Ⅱ)若{bn}为等差数列,先判断an≥n,再证明an≤n,即可求出所有可能的数列{an}.
(Ⅲ)确定b1,b2,依此类推,发现规律,得出bq,从而求出b1+b2+…+bq的值.
(Ⅱ)若{bn}为等差数列,先判断an≥n,再证明an≤n,即可求出所有可能的数列{an}.
(Ⅲ)确定b1,b2,依此类推,发现规律,得出bq,从而求出b1+b2+…+bq的值.
解答:
解:(Ⅰ)an≤1,则b1=1,an≤2,则b2=1,an≤3,则b3=3.
(Ⅱ)由题意,得1=a1<a2<…<an<…,得an≥n.
又∵使得an≤m成立的n的最大值为bm,使得an≤m+1成立的n的最大值为bm+1,
∴b1=1,bm≤bm+1.
设a2=k,则k≥2.
假设k>2,即a2=k>2,
则当n≥2时,an>2;当n≥3时,an≥k+1.
∴b2=1,bk=2.
∵{bn}为等差数列,
∴公差d=b2-b1=0,
∴bn=1,.
这与bk=2(k>2)矛盾,
∴a2=2.
又∵a1<a2<…<an<…,
∴b2=2,
由{bn}为等差数列,得bn=n.
因为使得使得an≤m成立的n的最大值为bm,
∴an≤n,由an≥n,得an=n
(Ⅲ)设a2=k(k>1)
∵a1<a2<…<an<…,
∴b1=b2=…bk-1=1且bk=2,
∴数列{bn}中等于1的项有(k-1)个,即(a2-a1)个,
设a3=l,(l>k)
则bk=bk+1=…bl-1=2,且bl=3,
∴数列{bn}中等于2的项有(l-k)个,即(a3-a2)个,
…
以此类推:数列{bn}中等于p-1的项有(ap-aq)个
∴b1+b2+…+bq=(a2-a1)+2(a3-a2)+…(p-1)(ap-ap-1)+p
=-a1-a2-…-ap+(p-1)ap+p
=pap+p-(a1+a2+…+ap)
=p(q+1)-A
即:b1+b2+…+=p(q+1)-A.
(Ⅱ)由题意,得1=a1<a2<…<an<…,得an≥n.
又∵使得an≤m成立的n的最大值为bm,使得an≤m+1成立的n的最大值为bm+1,
∴b1=1,bm≤bm+1.
设a2=k,则k≥2.
假设k>2,即a2=k>2,
则当n≥2时,an>2;当n≥3时,an≥k+1.
∴b2=1,bk=2.
∵{bn}为等差数列,
∴公差d=b2-b1=0,
∴bn=1,.
这与bk=2(k>2)矛盾,
∴a2=2.
又∵a1<a2<…<an<…,
∴b2=2,
由{bn}为等差数列,得bn=n.
因为使得使得an≤m成立的n的最大值为bm,
∴an≤n,由an≥n,得an=n
(Ⅲ)设a2=k(k>1)
∵a1<a2<…<an<…,
∴b1=b2=…bk-1=1且bk=2,
∴数列{bn}中等于1的项有(k-1)个,即(a2-a1)个,
设a3=l,(l>k)
则bk=bk+1=…bl-1=2,且bl=3,
∴数列{bn}中等于2的项有(l-k)个,即(a3-a2)个,
…
以此类推:数列{bn}中等于p-1的项有(ap-aq)个
∴b1+b2+…+bq=(a2-a1)+2(a3-a2)+…(p-1)(ap-ap-1)+p
=-a1-a2-…-ap+(p-1)ap+p
=pap+p-(a1+a2+…+ap)
=p(q+1)-A
即:b1+b2+…+=p(q+1)-A.
点评:本题考查等比数列的性质,考查学生对题意的理解,考查学生分析解决问题的能力,有难度

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
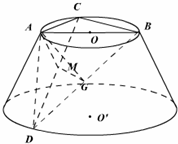 如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.
如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.