题目内容
已知函数f（x）=2
sinxcosx-2sin2x+a，a∈R．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若函数f（x）有零点，求实数a的取值范围．
| 3 |
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）若函数f（x）有零点，求实数a的取值范围．
考点：三角函数中的恒等变换应用,三角函数的周期性及其求法
专题：三角函数的图像与性质
分析：（Ⅰ）首先，利用二倍角公式，化简函数解析式，然后，利用周期公式确定该函数的最小正周期；
（Ⅱ）令f（x）=0，然后，结合三角函数的图象与性质进行求解．
（Ⅱ）令f（x）=0，然后，结合三角函数的图象与性质进行求解．
解答：
解：（Ⅰ）∵f（x）=
sin2x+cos2x+a-1
=2sin（2x+
）+a-1，
∴T=
=π，
∴函数f（x）的最小正周期为π．
（Ⅱ）令f（x）=0，即2sin（2x+
）+a-1=0，
则a=1-2sin（2x+
），
∵-1≤sin（2x+
）≤1，
∴-1≤1-2sin（2x+
）≤3，
∴若f（x）有零点，则实数a的取值范围是[-1，3]．
| 3 |
=2sin（2x+
| π |
| 6 |
∴T=
| 2π |
| 2 |
∴函数f（x）的最小正周期为π．
（Ⅱ）令f（x）=0，即2sin（2x+
| π |
| 6 |
则a=1-2sin（2x+
| π |
| 6 |
∵-1≤sin（2x+
| π |
| 6 |
∴-1≤1-2sin（2x+
| π |
| 6 |
∴若f（x）有零点，则实数a的取值范围是[-1，3]．
点评：本题重点考查了二倍角公式、三角恒等变换公式，三角函数的图象与性质等知识，考查比较综合，属于中档题．
练习册系列答案
相关题目
复数z=
（i为虚数单位）在复平面内对应点的坐标是（ ）
| 2+4i |
| 1-i |
| A、（3，3） |
| B、（-1，3） |
| C、（3，-1） |
| D、（2，4） |
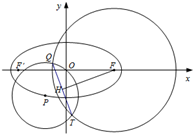在平面直角坐标系xOy中，已知椭圆
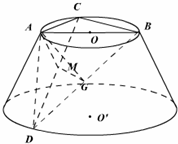如图所示，AB是圆台上底面⊙O的直径，C是⊙O上不同于A、B的一点，D是圆台下底面⊙O′上的一点，过A、B、C、D的截面垂直与底面，M是CD的中点，又AC=AD=2，∠CAD=120°，∠BCD=30°．