题目内容
已知函数f(x)=
,若对于正数kn(n∈N*),直线y=kn•x与函数y=f(x)的图象恰有2n+1个不同交点,则
(k12+k22+…+kn2)= .
|
| lim |
| n→∞ |
考点:函数的图象,分段函数的应用,极限及其运算
专题:综合题
分析:由函数f(x)是分段函数求出各段内的表达式,画出草图,得到直线和y=f(x)交点的规律,列方程组求出
的值,问题得解.
| k | 2 n |
解答:
解:∵当0≤x<2时,f(x)=
,
当2≤x<4时,0≤x-2<2,
∴f(x-2)=
=
,
当4≤x<6时,0≤x-4<6,
∴f(x-4)=
=
,
以此类推…,
∴函数f(x)的图象如图所示:

当n=1时,y=k1x与函数y=f(x)的图象恰有3个不同交点,
此时,y=k1x与第一个半圆相交与第二个半圆相切,
当n=2时,y=k2x与函数y=f(x)的图象恰有5个不同交点,
此时,y=k2x与前两个半圆相交与第三个半圆相切,…,
当n=n时,直线y=kn•x与函数y=f(x)的图象恰有2n+1个不同交点,
此时,y=knx与前n个半圆相交与第n+1个半圆相切,
于是有;
⇒(
x2+1)-2(2n+1)x+(2n+1)2-1=0
⇒△=[2(2n+1)]2-4
+1)[(2n+1)2-1]=0,
解得:
=
=
(
-
),
∴
+
+
+…+
=
(1-
+
-
+…+
-
)
=
(1-
),
则
(k12+k22+…+kn2)=
(1-
)=
.
| 1-(x-1)2 |
当2≤x<4时,0≤x-2<2,
∴f(x-2)=
| 1-[(x-2)-1]2 |
| 1-(x-3)2 |
当4≤x<6时,0≤x-4<6,
∴f(x-4)=
| 1-[(x-4)-1]2 |
| 1-(x-5)2 |
以此类推…,
∴函数f(x)的图象如图所示:

当n=1时,y=k1x与函数y=f(x)的图象恰有3个不同交点,
此时,y=k1x与第一个半圆相交与第二个半圆相切,
当n=2时,y=k2x与函数y=f(x)的图象恰有5个不同交点,
此时,y=k2x与前两个半圆相交与第三个半圆相切,…,
当n=n时,直线y=kn•x与函数y=f(x)的图象恰有2n+1个不同交点,
此时,y=knx与前n个半圆相交与第n+1个半圆相切,
于是有;
|
| k | 2 n |
⇒△=[2(2n+1)]2-4
| (k | 2 n |
解得:
| k | 2 n |
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
∴
| k | 2 1 |
| k | 2 2 |
| k | 2 3 |
| k | 2 n |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 4 |
| 1 |
| n+1 |
则
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| 4 |
点评:本题主要考察了分段函数,函数的图象及性质,数列裂项求和以及求极限值,是一道综合题.

练习册系列答案
相关题目
已知集合A={0,1,2,3,4},集合B={0,2,4,6,8},则A∩B=( )
| A、{0} |
| B、{0,4} |
| C、{2,4} |
| D、{0,2,4} |
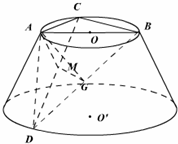 如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.
如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.