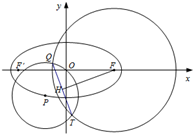
题目内容
已知椭圆x2+
=1的左、右两个顶点分别为A,B,曲线C是以A,B两点为顶点,焦距为2
的双曲线.设点P在第一象限且在曲线C上,直线AP与椭圆相交于另一点T.
(Ⅰ)求曲线C的方程;
(Ⅱ)设P,T两点的横坐标分别为x1,x2,求证:x1•x2为定值;
(Ⅲ)设△TAB与△POB(其中o为坐标原点)的面积分别为s1与s2,且
•
≤15,求s12-s22的取值范围.
| y2 |
| 4 |
| 5 |
(Ⅰ)求曲线C的方程;
(Ⅱ)设P,T两点的横坐标分别为x1,x2,求证:x1•x2为定值;
(Ⅲ)设△TAB与△POB(其中o为坐标原点)的面积分别为s1与s2,且
| PA |
| PB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆性质求出A(-1,0),B(1,0).由题意知双曲线的焦距2c=2
,实半轴a=1,由此能求出双曲线C的方程.
(Ⅱ)设点P(x1,y1),T(x2,y2)(x1>0,x2>0),则直线AP的方程为y=k(x+1),代入x2+
=1,得(4+k2)x2+2k2x+k2-4=0,由此能证明为x1•x2为定值.
(Ⅲ)由已知条件推导出
+
≤16,
≤4,从而得到1<x1≤2,由此能求出
-
的取值范围为[0,1].
| 5 |
(Ⅱ)设点P(x1,y1),T(x2,y2)(x1>0,x2>0),则直线AP的方程为y=k(x+1),代入x2+
| y2 |
| 4 |
(Ⅲ)由已知条件推导出
| x | 2 1 |
| y | 2 1 |
| x | 2 1 |
| s | 2 1 |
| s | 2 2 |
解答:
(Ⅰ)解:∵椭圆x2+
=1的左、右两个顶点分别为A,B,
∴A(-1,0),B(1,0).
∵曲线C是以A,B两点为顶点,焦距为2
的双曲线,
∴双曲线的焦距2c=2
,实半轴a=1,
∴c=
,b2=c2-a2=4.
∴双曲线C的方程为x2-
=1.
(Ⅱ)证明:设点P(x1,y1),T(x2,y2)(x1>0,x2>0),
直线AP的斜率为k(k>0),则直线AP的方程为y=k(x+1),
代入x2+
=1,
整理,得(4+k2)x2+2k2x+k2-4=0,
解得x=-1或x=
,
所以x2=
.
同理将直线方程代入x2-
=1,解得x1=
.
∴x1•x2=
•
=1为定值.
(Ⅲ)解:由(Ⅱ)知,
=(-1-x1,-y1),
=(1-x1,-y1),
又
•
≤15,
∴(-1-x1)(1-x1)+
≤15,即
+
≤16,
∵点P在双曲线上,则
-
=1,
∴
+4
-4≤16,即
≤4,
又点P是双曲线在第一象限内的点,∴1<x1≤2,
∵s1=
|AB||y2|=|y2|,s2=
|OB||y1|=
|y1|,
所以.
-
=
-
=(4-4
)-(
-1)=5-
-4
由(Ⅱ)知x1•x2=1,即,x2=
,
设t=
,则1<t≤4,
∴
-
=5-t-
,
∵t+
在(1,2]上单调递减,在[2,4]上单调递增,
∴当t=4,即x1=2时,(
-
)min=0.
当t=2,即x1=
.(
-
)max=1
∴
-
的取值范围为[0,1].
| y2 |
| 4 |
∴A(-1,0),B(1,0).
∵曲线C是以A,B两点为顶点,焦距为2
| 5 |
∴双曲线的焦距2c=2
| 5 |
∴c=
| 5 |
∴双曲线C的方程为x2-
| y2 |
| 4 |
(Ⅱ)证明:设点P(x1,y1),T(x2,y2)(x1>0,x2>0),
直线AP的斜率为k(k>0),则直线AP的方程为y=k(x+1),
代入x2+
| y2 |
| 4 |
整理,得(4+k2)x2+2k2x+k2-4=0,
解得x=-1或x=
| 4-k2 |
| 4+k2 |
所以x2=
| 4-k2 |
| 4+k2 |
同理将直线方程代入x2-
| y2 |
| 4 |
| 4+k2 |
| 4-k2 |
∴x1•x2=
| 4+k2 |
| 4-k2 |
| 4-k2 |
| 4+k2 |
(Ⅲ)解:由(Ⅱ)知,
| PA |
| PB |
又
| PA |
| PB |
∴(-1-x1)(1-x1)+
| y | 2 1 |
| x | 2 1 |
| y | 2 1 |
∵点P在双曲线上,则
| x | 2 1 |
| ||
| 4 |
∴
| x | 2 1 |
| x | 2 1 |
| x | 2 1 |
又点P是双曲线在第一象限内的点,∴1<x1≤2,
∵s1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以.
| s | 2 1 |
| s | 2 2 |
| y | 2 2 |
| 1 |
| 4 |
| y | 2 1 |
| x | 2 2 |
| x | 2 1 |
| x | 2 1 |
| x | 2 2 |
由(Ⅱ)知x1•x2=1,即,x2=
| 1 |
| x1 |
设t=
| x | 2 1 |
∴
| s | 2 1 |
| s | 2 2 |
| 4 |
| t |
∵t+
| 4 |
| t |
∴当t=4,即x1=2时,(
| s | 2 1 |
| s | 2 2 |
当t=2,即x1=
| 2 |
| s | 2 1 |
| s | 2 2 |
∴
| s | 2 1 |
| s | 2 2 |
点评:本题考查曲线方程的求法,考查两数乘积为定值的证明,考查两三角形面积的平方差的取值范围的求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
相关题目
已知f′(x)是 f(x)的导函数,则
=( )
| lim |
| t→0 |
| f(3)-f(3-t) |
| t |
| A、f′(3) |
| B、f′(t) |
| C、-f′(3) |
| D、-f′(t) |
 在平面直角坐标系xOy中,已知椭圆
在平面直角坐标系xOy中,已知椭圆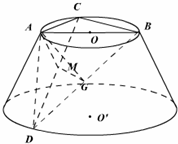 如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.
如图所示,AB是圆台上底面⊙O的直径,C是⊙O上不同于A、B的一点,D是圆台下底面⊙O′上的一点,过A、B、C、D的截面垂直与底面,M是CD的中点,又AC=AD=2,∠CAD=120°,∠BCD=30°.