题目内容
函数f（x）=x3+2x2-4x+5在[-4，1]上的最大值和最小值分别是（ ）
A、13，
| ||
| B、4，-11 | ||
| C、13，-11 | ||
| D、13，最小值不确定 |
考点：利用导数求闭区间上函数的最值
专题：导数的综合应用
分析：利用导数的运算法则可得极值点，再与区间端点进行比较即可得出最值．
解答：
解：f′（x）=3x2+4x-4=（3x-2）（x+2）=0，令f′（x）=0，∵x∈[-4，1]，∴x=-2或
．
列表如下：
由表格可知：当x=-2时，f（x）取得极大值，且f（-2）=13，又f（1）=4，因此最大值为13；当x=
时，f（x）取得极小值，且f（-4）=-11，又f（
）=
，因此最小值为-11．
综上可得：函数f（x）=x3+2x2-4x+5在[-4，1]上的最大值和最小值分别13，-11．
故选：C．
| 2 |
| 3 |
列表如下：
| x | [-4，-2） | -2 | (-2，
|
|
(
| ||||||
| f′（x） | + | 0 | - | 0 | + | ||||||
| f（x） | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
| 2 |
| 3 |
| 2 |
| 3 |
| 95 |
| 27 |
综上可得：函数f（x）=x3+2x2-4x+5在[-4，1]上的最大值和最小值分别13，-11．
故选：C．
点评：本题考查了闭区间上的连续函数的最值的求法，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
设函数f（x）=ex（sinx-cosx）（0≤x≤2014π），则函数f（x）的各极小值之和为（ ）
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
函数y=x3-3x的极大值为M极小值为N，则M+N=（ ）
| A、）4 | B、2 | C、1 | D、0 |
定义n!=1×2×…×n．如图是求10！的程序框图，则在判断框内应填的条件是（ ）
| A、i＜10 | B、i＞10 |
| C、i≤11 | D、i≤10 |
如果函数f（x）=
是奇函数，那么a=（ ）
| a•3x+2a-3 |
| 3x+1 |
| A、1 | ||
B、
| ||
| C、-1 | ||
| D、-2 |
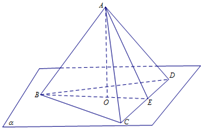如图，正三棱锥A-BCD放置在平面α上，AD=kCD，O是底面△BCD的中心，E是CD的中点，下列说法中，错误的是（ ）A、k＞
| ||||||||
B、当AD=CD=1时，将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动，且到点B的距离与到点侧面ACD的距离相等，则点P在抛物线弧上 | ||||||||
D、当k=
|
在极坐标系中，曲线C1：ρ（
cosθ+sinθ）=1与曲线C2：ρ=a（a＞0）的一个交点在极轴上，则a等于（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
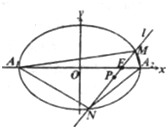已知椭圆C：