题目内容
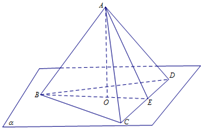 如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )
如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )A、k>
| ||||||||
B、当AD=CD=1时,将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动,且到点B的距离与到点侧面ACD的距离相等,则点P在抛物线弧上 | ||||||||
D、当k=
|
考点:命题的真假判断与应用,旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:
分析:A选项可以通过AB和BO的长度比较来判断k的取值范围,B选项可以通过求圆锥面积算出,C选项可以根据抛物线的性质确定,D选项可以通过投影面积的求法和适当的放缩来比较.
解答:
解:A选项,AD=AB>BO,假设BC边长为1,连接OC,则有∠OBC=∠OCB=30°,过D做BC的垂线交BC于H,则可知OC=DO=BO=2OH
∴BO=
BE,易求出BE=
∴BO=
∴k>
,A正确
B选项,旋转一周所得图形其实就是个圆锥形,底边圆的半径为r=BO=
,高A0可由直角三角形ABO求出,AO=
∴V体积=
×hS=
×
×π×(
)2=
π,B正确
C选项,通过分析可以看出,点P到面ACD的距离其实就是点P到线AE的距离,因为面ABE垂直面AEC,且交线为AE
∴通过抛物线的定义可知,抛物线到焦点的距离等于到准线的距离
∴P在抛物线上,C正确
D选项,易求出三角形BCD的面积为:SBCD=
,三角形ADC的面积为SADC=
,当绕CD转动时,我们假设转动的角度为a,则有面BCD在α的射影面积为:SBCD投影=
cosa,通过图象分析,我们发现当a小于一定角度时,面BCD和面ADC的投影面积是重合的,所以他们的射影面积和要小于当面ADC垂直面α时一起转动的射影面积之和.当面ADC垂直面α,然后转动的角度为a时,它的射影面积为SADC投影=
sina,所以他们的射影面积之和要小于:
cosa+
sina=
sin(a+β)≤
<
,所以D选项是错误的.
故选D
∴BO=
| 2 |
| 3 |
| ||
| 2 |
∴BO=
| ||
| 3 |
∴k>
| ||
| 3 |
B选项,旋转一周所得图形其实就是个圆锥形,底边圆的半径为r=BO=
| ||
| 3 |
| ||
| 3 |
∴V体积=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 27 |
C选项,通过分析可以看出,点P到面ACD的距离其实就是点P到线AE的距离,因为面ABE垂直面AEC,且交线为AE
∴通过抛物线的定义可知,抛物线到焦点的距离等于到准线的距离
∴P在抛物线上,C正确
D选项,易求出三角形BCD的面积为:SBCD=
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
故选D
点评:几何题先作图,然后根据各图形的特点做合理的运算

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
观察下列各式71=7,72=49,73=343,74=2401,75=16807,…,则72014的末尾两位数是( )
| A、01 | B、43 | C、49 | D、07 |
若α,β满足α-β=π,那么下列式子中正确的是( )
| A、sinα=sinβ |
| B、sinα=-sinβ |
| C、cosα=cosβ |
| D、cosα=sinβ |
函数f(x)=x3+2x2-4x+5在[-4,1]上的最大值和最小值分别是( )
A、13,
| ||
| B、4,-11 | ||
| C、13,-11 | ||
| D、13,最小值不确定 |
若三角形的三条边长分别为3,4,5,则将每条边长增加相同的长度后所得到的新三角形为( )
| A、直角三角形 | B、钝角三角形 |
| C、锐角三角形 | D、不能确定 |
可以用集合语言将“公理1:如果直线l上有两个点在平面α上,那么直线l在平面α上.”表述为( )
| A、A?l,B?l且A?α,B?α,则l?α |
| B、若A∈l,B∈l且A∈α,B∈α,则l∈α |
| C、若A∈l,B∈l且A∈α,B∈α,则l?α |
| D、若A∈l,B∈l且A?α,B?α,则l∈α |
已知平面α、β、γ,则下列命题中正确的是( )
| A、α⊥β,α∩β=a,a⊥b,则b⊥α |
| B、α⊥β,β⊥γ,则α∥γ |
| C、α∩β=a,β∩γ=b,α⊥β,则a⊥b |
| D、α∥β,β⊥γ,则α⊥γ |