题目内容
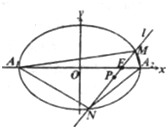 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
(1)求椭圆C的方程;
(2)记△A1MA2、△A1NA2的面积为S1、S2,若S1=2S2,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)将直线方程y=x-1代入椭圆方程
+
=1(a>b>0),得:(a2+b2)x2-2a2x+a2-a2b2=0,设M(x1,y1),N(x2,y2),由韦达定理求出kOP=
=-
=-
,由此能求出椭圆方程.
(2)联立方程组
,得:(4k2+3)x2-8k2x+4k2-12=0,由此利用韦达定理结合已知条件能求出直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| yP |
| xP |
| b2 |
| a2 |
| 3 |
| 4 |
(2)联立方程组
|
解答:
解:(1)将直线方程y=x-1代入椭圆方程
+
=1(a>b>0),
并整理得:(a2+b2)x2-2a2x+a2-a2b2=0,
设M(x1,y1),N(x2,y2),则x1,x2是方程的两个根,
由韦达定理得:x1+x2=
,x1x2=
,
y1+y2=x1+x2-2=
,
∴xP=
=
,yP=
=
,
∴kOP=
=-
,
∴由题意:-
=-
,∴3a2=4b2,
在直线l的方程中,令y=0,得x=1,
∴F(1,0),∴c=1,解得a2=4,b2=3,
∴椭圆方程为:
+
=1.…(6分)
(2)联立方程组
,
消元并整理得:(4k2+3)x2-8k2x+4k2-12=0,
△=(-8k2)2-4(4k2+3)( 4k2-12)=144(k2+1)>0
x1+x2=
,x1x2=
,
y1+y2=k(x1+x2-2)=
,y1y2=
,…①
S1=
|A1A2|•y1,S2=
|A1A2|•|y2|=-
|A1A2|•y2,
∵S1=2S2,∴y1=-2y2,
代入①中两个式子:-y2=
,…②
-2y2=
,…③
,得:
=-
,
整理得:
=
,∴k2=
,k=±
,
∴直线l方程为:
x-2y-
=0或
x+2y-
=0.…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
并整理得:(a2+b2)x2-2a2x+a2-a2b2=0,
设M(x1,y1),N(x2,y2),则x1,x2是方程的两个根,
由韦达定理得:x1+x2=
| 2a2 |
| a2+b2 |
| a2-a2b2 |
| a2+b2 |
y1+y2=x1+x2-2=
| -2b2 |
| a2+b2 |
∴xP=
| x1+x2 |
| 2 |
| a2 |
| a2+b2 |
| y1+y2 |
| 2 |
| -b2 |
| a2+b2 |
∴kOP=
| yP |
| xP |
| b2 |
| a2 |
∴由题意:-
| b2 |
| a2 |
| 3 |
| 4 |
在直线l的方程中,令y=0,得x=1,
∴F(1,0),∴c=1,解得a2=4,b2=3,
∴椭圆方程为:
| x2 |
| 4 |
| y2 |
| 3 |
(2)联立方程组
|
消元并整理得:(4k2+3)x2-8k2x+4k2-12=0,
△=(-8k2)2-4(4k2+3)( 4k2-12)=144(k2+1)>0
x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
y1+y2=k(x1+x2-2)=
| -6k |
| 4k2+3 |
| -9k2 |
| 4k2+3 |
S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵S1=2S2,∴y1=-2y2,
代入①中两个式子:-y2=
| -6k |
| 4k2+3 |
-2y2=
| -9k2 |
| 4k2+3 |
| ②2 |
| ① |
| ||
|
| 1 |
| 2 |
整理得:
| 4 |
| 4k2+3 |
| 1 |
| 2 |
| 5 |
| 4 |
| ||
| 2 |
∴直线l方程为:
| 5 |
| 5 |
| 5 |
| 5 |
点评:本题考查椭圆方程的求法,考查直线方程的求法,解题时要认真审题,注意根的判别式、韦达定理等知识点的合理运用.

练习册系列答案
相关题目
函数f(x)=x3+2x2-4x+5在[-4,1]上的最大值和最小值分别是( )
A、13,
| ||
| B、4,-11 | ||
| C、13,-11 | ||
| D、13,最小值不确定 |
已知平面α、β、γ,则下列命题中正确的是( )
| A、α⊥β,α∩β=a,a⊥b,则b⊥α |
| B、α⊥β,β⊥γ,则α∥γ |
| C、α∩β=a,β∩γ=b,α⊥β,则a⊥b |
| D、α∥β,β⊥γ,则α⊥γ |
 如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.