题目内容
对于函数f(x)=ex定义域中的任意的x1,x2(x1≠x2),有如下结论:
(1)f(x1x2)=f(x1)+f(x2);
(2)f(x1+x2)=f(x1)f(x2);
(3)
<0;
(4)
>0;
(5)f(
)<
.
上述结论中正确的序号是 .
(1)f(x1x2)=f(x1)+f(x2);
(2)f(x1+x2)=f(x1)f(x2);
(3)
| f(x1)-f(x2) |
| x1-x2 |
(4)
| f(x1)-f(x2) |
| x1-x2 |
(5)f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
上述结论中正确的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:根据指数函数f(x)=ex的运算性质,可以判定结论(1)错误,结论(2)正确;
又根据指数函数f(x)=ex的图象与性质,可以判定结论(3)错误,结论(4)正确;
又根据指数函数的值大于0,指数的运算性质以及基本不等式,可以判定结论(5)正确.
又根据指数函数f(x)=ex的图象与性质,可以判定结论(3)错误,结论(4)正确;
又根据指数函数的值大于0,指数的运算性质以及基本不等式,可以判定结论(5)正确.
解答:
解:∵对于函数f(x)=ex定义域中的任意的x1,x2(x1≠x2),
有f(x1x2)=ex1x2,f(x1)+f(x2)=ex1+ex2,
∴f(x1x2)≠f(x1)+f(x2),
∴结论(1)错误;
又f(x1+x2)=ex1+x2=ex1•ex2=f(x1)f(x2),
∴结论(2)正确;
又f(x)=ex是定义域R上的增函数,
∴对任意的x1,x2,不妨设x1<x2,则f(x1)<f(x2),
∴x1-x2<0,f(x1)-f(x2)<0,
∴
>0,
∴结论(3)错误,结论(4)正确;
又f(
)=e
,
=
;
∴
=
(
+
)
=
(e
-
+e
-
),
∵x1≠x2,
∴e
-
+e
-
>2,
∴
>1,
∴f(
)<
;
∴结论(5)正确;
综上,正确的结论是(2),(4),(5);
故答案为:(2),(4),(5).
有f(x1x2)=ex1x2,f(x1)+f(x2)=ex1+ex2,
∴f(x1x2)≠f(x1)+f(x2),
∴结论(1)错误;
又f(x1+x2)=ex1+x2=ex1•ex2=f(x1)f(x2),
∴结论(2)正确;
又f(x)=ex是定义域R上的增函数,
∴对任意的x1,x2,不妨设x1<x2,则f(x1)<f(x2),
∴x1-x2<0,f(x1)-f(x2)<0,
∴
| f(x1)-f(x2) |
| x1-x2 |
∴结论(3)错误,结论(4)正确;
又f(
| x1+x2 |
| 2 |
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
| ex1+ex2 |
| 2 |
∴
| ||
f(
|
| 1 |
| 2 |
| ex1 | ||
e
|
| ex2 | ||
e
|
=
| 1 |
| 2 |
| x1 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
| x1 |
| 2 |
∵x1≠x2,
∴e
| x1 |
| 2 |
| x2 |
| 2 |
| x2 |
| 2 |
| x1 |
| 2 |
∴
| ||
f(
|
∴f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∴结论(5)正确;
综上,正确的结论是(2),(4),(5);
故答案为:(2),(4),(5).
点评:本题考查了指数函数的图象与性质、指数的运算性质以及基本不等式的应用问题,解题的关键是熟练掌握这些基础知识并能灵活运用.

练习册系列答案
相关题目
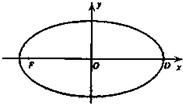 已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为
已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为
 如图,在圆的内接四边形ABCD中,∠ABC=90°,∠ABD=30°,∠BDC=45°,AD=1,则BC=
如图,在圆的内接四边形ABCD中,∠ABC=90°,∠ABD=30°,∠BDC=45°,AD=1,则BC= 如图,⊙O的直径AB=6,P是AB延长线上的一点,过P作⊙O的切线PC,连接AC,若∠CPA=30°,则点O到AC的距离等于
如图,⊙O的直径AB=6,P是AB延长线上的一点,过P作⊙O的切线PC,连接AC,若∠CPA=30°,则点O到AC的距离等于