题目内容
如图，⊙O的直径AB=6，P是AB延长线上的一点，过P作⊙O的切线PC，连接AC，若∠CPA=30°，则点O到AC的距离等于考点：与圆有关的比例线段
专题：直线与圆
分析：连结BC，OC，作OD⊥AC，交AC于D，由已知条件推导出BC=OB=OC=OA=3，∠A=30°，∠ACB=∠ADO=90°，由此能求出点O到AC的距离．
解答：
解：如图，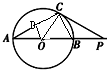
连结BC，OC，作OD⊥AC，交AC于D，
∵⊙O的直径AB=6，P是AB延长线上的一点，
过P作⊙O的切线PC，连接AC，∠CPA=30°，
∴BC=OB=OC=OA=3，∠A=30°，
∠ACB=∠OCP=∠ADO=90°，
∴AC=
=3
，AD=
，
∴点O到AC的距离OD=
=
．
故答案为：
．
连结BC，OC，作OD⊥AC，交AC于D，∵⊙O的直径AB=6，P是AB延长线上的一点，
过P作⊙O的切线PC，连接AC，∠CPA=30°，
∴BC=OB=OC=OA=3，∠A=30°，
∠ACB=∠OCP=∠ADO=90°，
∴AC=
| 62-32 |
| 3 |
3
| ||
| 2 |
∴点O到AC的距离OD=
32-(
|
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查点到直线距离的求法，是中档题，解题时要认真审题，注意弦切角定理的合理运用．
练习册系列答案
名校通行证有效作业系列答案
相关题目
已知椭圆方程为
+
=1（a＞b＞0），A、B分别是椭圆长轴的两个端点，M、N是椭圆上关于x轴对称的两点，直线AM，BN的斜率分别为k1，k2，若|k1•k2|=
，则椭圆的离心率为 ．
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
设等差数列{an}的前n项和为Sn，已知（a5-1）3+2009（a5-1）=1，（a2005-1）3+2009（a2005-1）=-1，则下列结论中正确的是（ ）
| A、S2009=2009，a2005＜a5 |
| B、S2009=2009，a2005＞a5 |
| C、S2009=-2009，a2005≤a5 |
| D、S2009=-2009，a2005≥a5 |