题目内容
已知平面内的动点P到两定点M(-2,0)、N(1,0)的距离之比为2:1.
(Ⅰ)求P点的轨迹方程;
(Ⅱ)过M点作直线,与P点的轨迹交于不同两点A、B,O为坐标原点,求△OAB的面积的最大值.
(Ⅰ)求P点的轨迹方程;
(Ⅱ)过M点作直线,与P点的轨迹交于不同两点A、B,O为坐标原点,求△OAB的面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设P(x,y),由已知条件利用两点间距离公式得
=2
,由此能求出P点的轨迹方程.
(Ⅱ)设直线AB方程为y=k(x+2),由
,得(1+k2)x2+4(k2-1)x+4k2=0,由△>0,得到0<k2<
,由此能求出△OAB的面积的最大值.
| (x+2)2+y2 |
| (x-1)2+y2 |
(Ⅱ)设直线AB方程为y=k(x+2),由
|
| 1 |
| 3 |
解答:
(本题满分14分)
解:(Ⅰ)设P(x,y),
∵动点P到两定点M(-2,0)、N(1,0)的距离之比为2:1,
∴|PM|=2|PN|,
∴
=2
,
化简得(x-2)2+y2=4,
∴所求的P点的轨迹方程为(x-2)2+y2=4.…(5分)
(Ⅱ)由题设知直线AB斜率存在且不为零,
设直线AB方程为y=k(x+2)(k≠0)
由
,消去y得,(1+k2)x2+4(k2-1)x+4k2=0,
由△=16(k2-1)2-16k2(1+k2)=16(1-3k2)>0,
解得k2<
.
∴0<k2<
,…(8分)
,
S△OAB=S△OMB-S△OMA
=
×2|y1-y2|
=|k||x1-x2|
=|k|
=4
=4
,…(11分)
令t=
,考察函数f(t)=-4t2+7t-3,t∈(
,1)
f(t)=-4t2+7t-3
=-4(t-
)2+
≤
,
当t=
,即t=±
时取等号,
此时Smax=1,即△OAB的面积的最大值为1.…(14分)
解:(Ⅰ)设P(x,y),
∵动点P到两定点M(-2,0)、N(1,0)的距离之比为2:1,
∴|PM|=2|PN|,
∴
| (x+2)2+y2 |
| (x-1)2+y2 |
化简得(x-2)2+y2=4,
∴所求的P点的轨迹方程为(x-2)2+y2=4.…(5分)
(Ⅱ)由题设知直线AB斜率存在且不为零,
设直线AB方程为y=k(x+2)(k≠0)
由
|
由△=16(k2-1)2-16k2(1+k2)=16(1-3k2)>0,
解得k2<
| 1 |
| 3 |
∴0<k2<
| 1 |
| 3 |
|
S△OAB=S△OMB-S△OMA
=
| 1 |
| 2 |
=|k||x1-x2|
=|k|
| (x1+x2)2-4x1x2 |
=4
|
=4
|
令t=
| 1 |
| t2+1 |
| 3 |
| 4 |
f(t)=-4t2+7t-3
=-4(t-
| 7 |
| 8 |
| 1 |
| 16 |
| 1 |
| 16 |
当t=
| 7 |
| 8 |
| ||
| 7 |
此时Smax=1,即△OAB的面积的最大值为1.…(14分)
点评:本题考查点的轨迹方程的求法,考查三角形面积的最大值的求法,解题时要注意函数与方程思想的合理运用.

练习册系列答案
相关题目
z=x-y在
的线性约束条件下,取得最大值的可行解为( )
|
| A、(0,1) | ||||
| B、(-1,-1) | ||||
| C、(1,0) | ||||
D、(
|
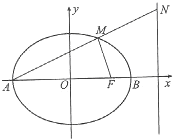 如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且
如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且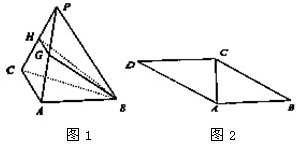 已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点.
已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点.