题目内容
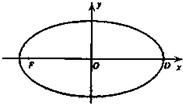 已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为F(-
已知在平面直角坐标系xOy中的一个椭圆C,它的中心在原点,左焦点为F(-| 3 |
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设不过原点的直线l:y=x+m与椭圆C交于A,B两点.
①求实数m的取值范围;
②求实数m取何值时△AOB的面积最大,△AOB面积的最大值是多少?
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件设椭圆方程为
+
=1,且a=2,c=
,由此能求出椭圆方程.
(Ⅱ)①把直线l的方程y=x+m代入椭圆方程
+y2=1,得5x2+8mx+4(m2-1)=0,由已和条件利用根的判别式能求出实数m的取值范围.
②设A(x1,y1),B(x2,y2),由已知条件推导出|AB|=
,原点到直线AB的距离为
,由此能求出当m=±
时,△AOB面积最大值等于1.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅱ)①把直线l的方程y=x+m代入椭圆方程
| x2 |
| 4 |
②设A(x1,y1),B(x2,y2),由已知条件推导出|AB|=
| 2(x1-x2)2 |
| |m| | ||
|
| ||
| 2 |
解答:
解:(Ⅰ)设所求的椭圆方程为
+
=1(a>b>0),
∵左焦点为F(-
,0),右顶点为D(2,0),
∴a=2,c=
,
∴a2-b2=3,∴b=1,
∴椭圆方程为
+y2=1.
(Ⅱ)①把直线l的方程y=x+m代入椭圆方程
+y2=1,
整理,得5x2+8mx+4(m2-1)=0,
依题意,由△>0,得(8m)2-4×5×4(m2-1)>0,
∴16(5-m2)>0,∴-
<m<
,
又∵m≠0,∴-
<m<0或0<m<
.
∴实数m的取值范围是{m|-
<m<0或0<m<
}.
②设A(x1,y1),B(x2,y2),则由①得:
x1+x2=-
,x1•x2=
,
又∵|AB|=
=
,
原点到直线AB的距离为
,
∴S△AOB=
•|AB|•
=
×
×
•|m|
=
≤
•
=1,
当且仅当m2=5-m2,即m=±
∈(-
,0)∪(0,
)时等号成立.
∴当m=±
时,△AOB面积最大值等于1.
| x2 |
| a2 |
| y2 |
| b2 |
∵左焦点为F(-
| 3 |
∴a=2,c=
| 3 |
∴a2-b2=3,∴b=1,
∴椭圆方程为
| x2 |
| 4 |
(Ⅱ)①把直线l的方程y=x+m代入椭圆方程
| x2 |
| 4 |
整理,得5x2+8mx+4(m2-1)=0,
依题意,由△>0,得(8m)2-4×5×4(m2-1)>0,
∴16(5-m2)>0,∴-
| 5 |
| 5 |
又∵m≠0,∴-
| 5 |
| 5 |
∴实数m的取值范围是{m|-
| 5 |
| 5 |
②设A(x1,y1),B(x2,y2),则由①得:
x1+x2=-
| 8m |
| 5 |
| 4(m2-1) |
| 5 |
又∵|AB|=
| (1+k2)(x1-x2)2 |
| 2(x1-x2)2 |
原点到直线AB的距离为
| |m| | ||
|
∴S△AOB=
| 1 |
| 2 |
| |m| | ||
|
| 1 |
| 2 |
| 4 |
| 5 |
| 5-m2 |
=
| 2 |
| 5 |
| m2•(5-m2) |
≤
| 2 |
| 5 |
| m2+(5-m2) |
| 2 |
当且仅当m2=5-m2,即m=±
| ||
| 2 |
| 5 |
| 5 |
∴当m=±
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查实数的取值范围的求法,考查三角形面积的最大值的求法,解题时要注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
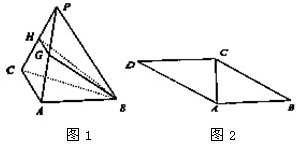 已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点.
已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点. 已知椭圆C:
已知椭圆C: