题目内容

已知函数f（x）=4x2-mx+5在（-∞，2）上是减函数，则实数m的取值范围
 
．
考点：二次函数的性质
专题：函数的性质及应用
分析：根据二次函数的单调性与开口方向和对称轴有关，先求出函数的对称轴，然后结合开口方向可知（-∞，2）是（-∞，
m
8
）的子集即可．
解答： 解：二次函数f（x）=4x2-mx+5是开口向上的二次函数
对称轴为x=
m
8
，
∴二次函数f（x）=4x2-mx+5在（-∞，
m
8
）上减增函数
∵函数f（x）=4x2-mx+5在（-∞，2）上是减函数，
∴2≤
m
8

即m≥16
故答案为：m≥16
点评：本题主要考查了二次函数的单调性，二次函数是高考中的热点问题，属于基础题．
练习册系列答案
相关题目
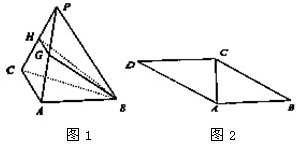已知平行四边形ABCD （如图1）中，AB=4，BC=5，对角线AC=3，将三角形△ACD沿AC折起至△PAC位置（图2），使二面角P-AC-B为60°，G，H分别是PA，PC的中点．
（Ⅰ）求证：PC⊥平面BGH；
（Ⅱ）求平面PAB与平面BGH夹角的余弦值．
对于函数f（x）=ex定义域中的任意的x1，x2（x1≠x2），有如下结论：
（1）f（x1x2）=f（x1）+f（x2）；    
（2）f（x1+x2）=f（x1）f（x2）；
（3）
f(x1)-f(x2)
x1-x2
＜0；       
 (4)
f(x1)-f(x2)
x1-x2
＞0；
（5）f(
x1+x2
2
)＜
f(x1)+f(x2)
2
．
上述结论中正确的序号是
 
．
若一个命题的逆命题、否命题、逆否命题中有且只有一个是真命题，我们就把这个命题叫做“正向真命题”，给出下列命题：
①函数y=x2（x∈R）为偶函数；   
②若
a
•
c
=
b
•
c
，则
a
=
b

③若四点不共面，则这四点中任何三点都不共线；
其中是“正向真命题”的是
 
．
已知实数x，y满足
x+y-3≥0
x+2y-5≤0
y≥0
，则z=（x-1）2+y2的最小值是
 
．
函数y=
x
x+1
的值域为
 
．
科拉茨是德国数学家，他在1937年提出了一个著名的猜想：任给一个正整数n，如果n是偶数，就将它减半（即
n
2
）；如果n是奇数，则将它乘3加1（即3n+1），不断重复这样的运算，经过有限步后，一定可以得到1．如初始正整数为6，按照上述变换规则，我们可以得到一个数列：6，3，10，5，16，8，4，2，1．
（1）如果n=2，则按照上述规则施行变换后的第8项为
 

（2）如果对正整数n（首项）按照上述规则施行变换后的第8项为1（注：1可以多次出现），则n的所有不同值的个数为
 
．
下列命题中正确的个数是（　　）
（1）若
a
为单位向量，且
b
∥
a
，|
b
|=1，则
a
=
b
；   
（2）若|
a
|=0，则
a
=0
（3）若
b
∥
a
，则|
b
|=|
a
|；   
（4）若k
a
=
0
，则必有k=0（k∈R）；   
（5）若k∈R，则k•
0
=0．
A、0B、1C、2D、3
对于平面直角坐标系内任意两点A（x1，y1），B（x2，y2），定义它们之间的一种“折线距离”：
d（A，B）=|x2-x1|+|y2-y1|．则下列命题正确的个数是（　　）
①若A（-1，3），B（1，0），则d（A，B）=5；
②若点C在线段AB上，则d（A，C）+d（C，B）=d（A，B）；
③在△ABC中，一定有d（A，C）+d（C，B）＞d（A，B）；
④在平行四边形ABCD中，一定有d（A，B）+d（A，D）=d（C，B）+d（C，D）．
A、1个B、2个C、3个D、4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网