题目内容
已知双曲线
-
=1(a>0,b>0)的一条渐近线经过点(2,2
),则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线
-
=1(a>0,b>0)的一条渐近线经过点(2,2
),可得
=
=
,利用e2=1+(
)2,可求双曲线的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| b |
| a |
2
| ||
| 2 |
| 3 |
| b |
| a |
解答:
解:∵双曲线
-
=1(a>0,b>0)的一条渐近线经过点(2,2
),
∴
=
=
,
∴e2=1+(
)2=4,
∴e=2.
故选:B.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
∴
| b |
| a |
2
| ||
| 2 |
| 3 |
∴e2=1+(
| b |
| a |
∴e=2.
故选:B.
点评:本题考查双曲线的几何性质,考查学生的计算能力,正确运用双曲线
-
=1(a>0,b>0)的一条渐近线经过点(2,2
)是关键.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |

练习册系列答案
相关题目
下列命题中正确的个数是( )
(1)若
为单位向量,且
∥
,|
|=1,则
=
;
(2)若|
|=0,则
=0
(3)若
∥
,则|
|=|
|;
(4)若k
=
,则必有k=0(k∈R);
(5)若k∈R,则k•
=0.
(1)若
| a |
| b |
| a |
| b |
| a |
| b |
(2)若|
| a |
| a |
(3)若
| b |
| a |
| b |
| a |
(4)若k
| a |
| 0 |
(5)若k∈R,则k•
| 0 |
| A、0 | B、1 | C、2 | D、3 |
i是虚数单位,复数z=
=( )
| 2-i |
| 1-i |
A、
| ||||
B、
| ||||
| C、1+3i | ||||
| D、3-i |
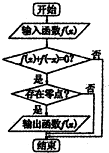
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )

| A、f(x)=x2-1 | ||
B、f(x)=
| ||
C、f(x)=
| ||
| D、f(x)=3sinx+1 |
设等差数列{an}的前n项和为Sn,已知(a5-1)3+2009(a5-1)=1,(a2005-1)3+2009(a2005-1)=-1,则下列结论中正确的是( )
| A、S2009=2009,a2005<a5 |
| B、S2009=2009,a2005>a5 |
| C、S2009=-2009,a2005≤a5 |
| D、S2009=-2009,a2005≥a5 |