题目内容
已知等差数列{an}的前9项和为153.
(1)数列{an}中是否存在确定的项?若存在,求出该确定的项,若不存在,请说明理由.
(2)若a2=8,从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,按原来的顺序构成新数列{bn},求数列{bn}的前n项和Tn,并求使m•(an-2)<Tn+6恒成立的最大正整数m.
(1)数列{an}中是否存在确定的项?若存在,求出该确定的项,若不存在,请说明理由.
(2)若a2=8,从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,按原来的顺序构成新数列{bn},求数列{bn}的前n项和Tn,并求使m•(an-2)<Tn+6恒成立的最大正整数m.
考点:数列与不等式的综合,等差数列的性质
专题:等差数列与等比数列
分析:(1)S9=
(a1+a9)=9a5=153,由此能求出数列{an}中存在确定的项.
(2)由a2=8,a5=17,得an=3n+2,利用分组求和法能求出Tn=3•2n+1+2n-6,由此能求出使m•(an-2)<Tn+6恒成立的最大正整数m.
| 9 |
| 2 |
(2)由a2=8,a5=17,得an=3n+2,利用分组求和法能求出Tn=3•2n+1+2n-6,由此能求出使m•(an-2)<Tn+6恒成立的最大正整数m.
解答:
解:(1)∵等差数列{an}的前9项和为153,
∴S9=
(a1+a9)=9a5=153,
解得a5=17.
∴数列{an}中存在确定的项a5=17.
(2)∵a2=8,a5=17,
∴d=
=3,an=8+(n-2)×3=3n+2,
∴a2n=3×2n+2,
Tn=a2+a4+a8+…+a 2n
=3(2+4+8+…+2n)+2n
=3×
+2n
=3•2n+1+2n-6.
∵m•(an-2)<Tn+6,
∴m<
-
.
∴当n=1或n=2时,m<4-
=
,
∴使m•(an-2)<Tn+6恒成立的最大正整数m=3.
∴S9=
| 9 |
| 2 |
解得a5=17.
∴数列{an}中存在确定的项a5=17.
(2)∵a2=8,a5=17,
∴d=
| 17-8 |
| 5-2 |
∴a2n=3×2n+2,
Tn=a2+a4+a8+…+a 2n
=3(2+4+8+…+2n)+2n
=3×
| 2(1-2n) |
| 1-2 |
=3•2n+1+2n-6.
∵m•(an-2)<Tn+6,
∴m<
| 2n+1 |
| n |
| 2 |
| 3 |
∴当n=1或n=2时,m<4-
| 2 |
| 3 |
| 10 |
| 3 |
∴使m•(an-2)<Tn+6恒成立的最大正整数m=3.
点评:本题考查数列中是否存在确定的项的判断与求法,考查使m•(an-2)<Tn+6恒成立的最大正整数m的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
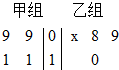 以下茎叶图记录了甲、乙两组各四名同学的植树棵树. 乙组记录中有一个数据模糊,无法辨认,在图中以X表示.
以下茎叶图记录了甲、乙两组各四名同学的植树棵树. 乙组记录中有一个数据模糊,无法辨认,在图中以X表示. 棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体AC1中,设M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.