题目内容
已知关于x的不等式(x-a)(x-a-2)≤0的解集为A,集合B={x|-2≤x≤2}.若“x∈A”是“x∈B”的充分不必要条件,则实数a的取值范围是 .
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的性质求出p,q对应的等价条件,利用充分条件和必要条件的定义建立条件关系即可得到结论.
解答:
解:A={x|a≤x≤a+2},B={x|-2≤x≤2}.
“x∈A”是“x∈B”的充分不必要条件,
则A是B的真子集,
∴
,
解得-2≤a≤0,
即实数a的取值范围是[-2,0]
“x∈A”是“x∈B”的充分不必要条件,
则A是B的真子集,
∴
|
解得-2≤a≤0,
即实数a的取值范围是[-2,0]
点评:本题主要考查充分条件和必要条件的应用,利用不等式的解法是解决本题的关键,比较基础

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知两定点F1(-1,0)、F2(1,0),则命题甲:|F1F2|是|PF1|与|PF2|的等差中项,命题乙:动点P的轨迹是椭圆,则甲是乙的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
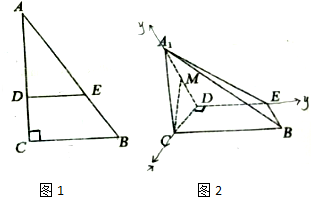 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,DE分别为AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.求证:A1C⊥平面BCDE.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,DE分别为AC、AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.求证:A1C⊥平面BCDE.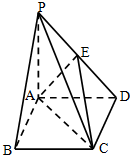 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.