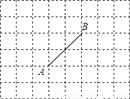
在所给的8×6网格图中，横竖每相邻两点间的长度均为1，以这些点为顶点的三角形称为网格三角形，请找出点M，使以A，B，M为顶点的网格三角形是直角三角形，这样的点M有_______个．
12
【解析】如图，在线段CD和线段EF上各有5个符合条件的点，图中的两个M点也符合要求，所以符合条件的点M共有12个. 如图，点A2，A4…分别是x轴上的点，点A1，A3，A5，…分别是射线OA2n-1上的点，△OA1A2，△OA2A3，△OA3A4，…分别是以OA2，OA3，OA4 ，OA5…为底边的等腰三角形，若OA2n-1与x轴正半轴的夹角为30°，OA1=1，则可求得点A2的坐标是________；A2n-1的坐标_______.
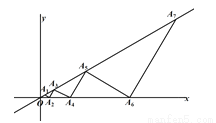
【解析】根据等腰三角形的三线合一的性质和30°角直角三角形的性质可求得, ,再由等腰三角形的三线合一的性质和30°角直角三角形的性质可求得， ，由此可得A2n-1的坐标. 解下列不等式组并把解在数轴上表示出来.
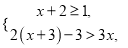
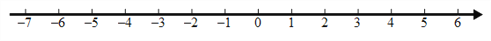
，在数轴上表示见解析.
【解析】试题分析：分别求出两个不等式的解集，这两个不等式解集的公共部分即为不等式组的解集，在数轴上表示出来即可.
试题解析：
由（1）得，
由（2）得，
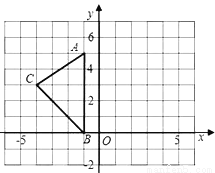
不等式组的解集在数轴上表示如下： 如图，在平面直角坐标系XOY中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）计算△ABC的面积．
（1)画图见解析；（2）7.5
【解析】试题分析：（1）从三角形的各顶点向y轴引垂线并延长相同长度，找对应点．顺次连接即可；（2）根据网格可以看出三角形的底AB是5，高是C到AB的距离，是3，利用面积公式计算．
试题解析：
（1）如图所示：
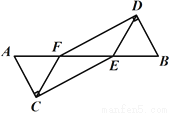
（2）S△ABC=×5×3= （或7.5）（平方单位）． 如图，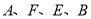 
四点共线，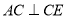 
， 
， 
， 
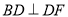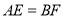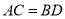.求证：CE∥DF.
证明见解析.
【解析】试题分析：利用HL证明RtΔACE?RtΔBDF，根据全等三角形的性质即可得∠AEC=∠BFD，由内错角相等，两直线平行即可得CE∥DF.
试题解析：
∵AC⊥CE,BD⊥DF，
∴∠ACE=∠BDF=90°，
又∵AE=BF,AC=BD，
∴RtΔACE?RtΔBDF(HL)，
∴∠AEC=∠BFD，
∴CE∥DF.
... 如图，在平面直角坐标系内，四边形OECB的顶点坐标分别是：B（2，5），C（8，5），E（10，0），点P（x，0）是线段OE上一点，设四边形BPEC的面积为S．
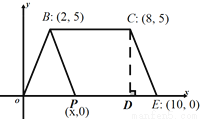
（1）过点C作CD⊥x轴于点E，则CD= ， 用含x的代数式表示PE= .
（2）求S与x的函数关系．
（3）当S＝30时，直接写出线段PE与PB的长．
（1）CD=5，PE=10-x；（2）（3）PE=6，PB=
【解析】试题分析：（1）根据点D的坐标直接求得CD的长，根据点E的坐标表示出PE的长即可；（2）根据已知条件可知四边形BPEC是梯形，利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值，即可求得PE的长，过点B作BM⊥X轴于点M，在Rt△BPM中，根据勾股定理求得PB的长即可.
试题解析：
（1）CD=5，P... 如图，直线y＝kx＋b经过点A(5，0)，B(1，4)．
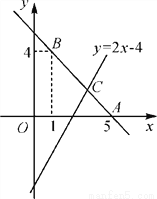
（1）求直线AB的表达式；
（2）若直线y＝2x－4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式kx＋b＞2x－4>0的解集．
（1）y=-x+5；（2）C（3，2）；（3）2在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
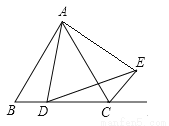
（1）如图一，若△ABC是等边三角形，且AB=AC=2,点D在线段BC上，
①求证：∠BCE+∠BAC=180°；
②当四边形ADCE的周长取最小值时，求BD的长．
（2）若∠BAC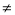
60° ，当点D在射线BC上移动，则∠BCE和∠BAC 之间有怎样的数量关系？并说明理由.
（1）①证明见解析；②BD=2；（2），理由见解析.
【解析】试题分析：
（1）∵
∴
又∵AB=AC，AD=AE
∴△ABD ≌ △ACE
∴
∴
（2）∵
∴
四边形ADCE的周长=AD+DC+CE+AE= AD+DC+BD+AE=BC+2AD.
∴ 即AD 时周长最小
∴
（3）∴
理由如下：
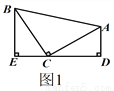
∴ 又∵... 【模型建立】
（1）如图1，等腰直角三角形ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过A作AD⊥ED于点D，过B作BE⊥ED于点E．求证：△BEC≌△CDA；
【模型应用】
（2）如图2，一次函数y=﹣2x+2的图象与y轴交于点A，与x轴交于点B，过点B作线段BC⊥AB且BC=AB，直线AC交x轴于点D．
①求点C的坐标，并直接写出直线AC的函数关系式；
②若点Q是图2中坐标平面内一点，当以点A，D，Q为顶点的三角形是等腰直角三角形时，直接写出点Q的坐标.
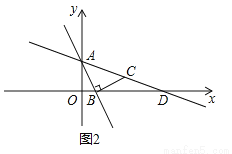
（1）证明见解析；
（2）①；②
【解析】试题分析：